Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
a) 3x -11 = 0 <=> 3x = 11 <=> x = 113113
<=> x ≈ 3, 67
Nghiệm gần đúng là x = 3,67.
b) 12 + 7x = 0 <=> 7x = -12 <=> x = −127−127
<=> x ≈ -1,71
Nghiệm gần đúng là x = -1,71.
c) 10 - 4x = 2x - 3 <=> -4x - 2x = -3 - 10
<=> -6x = -13 <=> x = 136136 <=> x ≈ 2,17
Nghiệm gần đúng là x = 2, 17.
Hướng dẫn giải:
a) Sai ở phương trình thứ hai chuyển vế hạng tử -6 từ vế trái sang vế phải, hạng tử -x từ vế phải sang vế trái mà không đổi dấu.
Giải lại: 3x - 6 + x = 9 - x
<=> 3x + x + x = 9 + 6
<=> 5x = 15
<=> x = 3
Vậy phương trình có nghiệm duy nhất x = 3
b) Sai ở phương trình thứ hai, chuyển vế hạng tử -3 từ vế trái sang vế phải mà không đổi dấu.
Giải lại: 2t - 3 + 5t = 4t + 12
<=> 2t + 5t - 4t = 12 + 3
<=> 3t = 15
<=> t = 5
Vậy phương trình có nghiệm duy nhất t = 5

Bài 3: (SBT/24):
a. \(\dfrac{5x+3}{x-2}\)=\(\dfrac{5x^2+13x+6}{x^2-4}\)
(5x+3) . (x2-4) = 5x3-20x+3x3-12
(x-2) . (5x2+13x+6) = 5x3+13x2+6x-10x2-26x-12 = 5x3-20x+3x2-12
=> (5x+3) (x2-4) = (x-2) (5x2+13x+6)
Vậy \(\dfrac{5x+3}{x-2}\)=\(\dfrac{5x^2+13x+6}{x^2-4}\)(đẳng thức đúng)
b. \(\dfrac{x+1}{x+3}\)=\(\dfrac{x^2+3}{x^2+6x+9}\)
(x+1) . (x2+6x+9) = x3+6x2+9x+x2+6x+9 = x3+7x2+15x+9
(x+3) . (x2+3) = x3+3x+3x2+9
=> (x+1) (x2+6x+9) ≠ (x+3) (x2+3)
Vậy \(\dfrac{x+1}{x+3}\)≠\(\dfrac{x^2+3}{x^2+6x+9}\)(đẳng thức sai)
Chữa lại: \(\dfrac{x+1}{x+3}\)=\(\dfrac{x^2+3}{x^{2_{ }}+6x+9}\)
c. \(\dfrac{x^2-2}{x^2-1}\)=\(\dfrac{x+2}{x+1}\)
(x2-2) . (x+1) = x3+x2-2x-2
(x2-1) . (x+2) = x3+2x2-x-2
=> (x2-2) (x+1) ≠ (x2-1) (x+2)
Vậy \(\dfrac{x^2-2}{x^2-1}\)≠\(\dfrac{x+2}{x+1}\)(đẳng thức sai)
Chữa lại: \(\dfrac{x^2+x-2}{x^2-1}\)=\(\dfrac{x+2}{x+1}\)
d. \(\dfrac{2x^2-5x+3}{x^2+3x-4}\)=\(\dfrac{2x^2-x-3}{x^2+5x+4}\)
(2x2-5x+3) . (x2+5x+4) = 2x4+10x3+8x2-5x3-25x2-20x+3x2+15x+12
= 2x4+5x3-14x2-5x+12
(x2+3x-4) . (2x2-x-3) = 2x4-x3-3x2+6x3-3x2-9x-8x2+4x+12
= 2x4+5x3-14x2-5x+12
=> (2x2-5x+3) (x2+5x+4) = (x2+3x-4) (2x2-x-3)
Vậy \(\dfrac{2x^2-5x+3}{x^2+3x-4}\)=\(\dfrac{2x^2-x-3}{x^2+5x+4}\)

sai ở chỗ là chia cả hai vế cho x-1 nên đã làm mất nghiệm.
giải lại:
\(\left(x-1\right)=\left(x-1\right)\left(x-3\right)\)
\(\Leftrightarrow\left(x-1\right)-\left(x-1\right)\left(x-3\right)=0\).
\(\Leftrightarrow\left(x-1\right)\left(1-x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4-x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=4\end{cases}}\)

1) (2x - 3)2 = 4x2 - 8
<=> 4x2 - 12x + 9 = 4x2 - 8
<=> 12x + 9 = -8
<=> 12x = -17
<=> x = 17/12
1) (2x - 3)^2 = 4x^2 - 8
<=> 4x^2 - 12x + 9 = 4x^2 - 8
<=> 4x^2 - 12x + 9 - 4x^2 = -8
<=> -12x + 9 = -8
<=> -12x = -8 - 9
<=> -12x = -17
<=> x = 17/12
2) x - (x + 2)(x - 3) = 4 - x^2
<=> x - x^2 + 3x - 2x + 6 = 4 - x^2
<=> 2x - x^2 + 6 = 4 - x^2
<=> 2x - x^2 + 6 + x^2 = 4
<=> 2x + 6 = 4
<=> 2x = 4 + 6
<=> 2x = 10
<=> x = 5
3) 3x - (x - 3)(x + 1) = 6x - x^2
<=> 3x - x^2 - x + 3x + 3 = 6x - x^2
<=> 5x - x^2 + 3 = 6x - x^2
<=> 5x - x^2 + 3 + x^2 = 6x
<=> 5x + 3 = 6x
<=> 3 = 6x - 5x
<=> 3 = x
4) 3x/4 = 6
<=> 3x = 6.4
<=> 3x = 24
<=> x = 8
5) 7 + 5x/3 = x - 2
<=> 21 + 5x = 3x - 6
<=> 5x = 3x - 6 - 21
<=> 5x = 3x - 27
<=> 5x - 3x = -27
<=> 2x = -27
<=> x = -27/2
6) x + 4 = 2/5x - 3
<=> 5x + 20 = 2x - 15
<=> 5x + 20 - 2x = -15
<=> 3x + 20 = -15
<=> 3x = -15 - 20
<=> 3x = -35
<=> x = -35/3
7) 1 + x/9 = 4/3
<=> x/9 = 4/3 - 1
<=> x/9 = 1/3
<=> x = 3

\(2x-2=8-3x\)
\(\Leftrightarrow\)\(2x+3x=8+2\)
\(\Leftrightarrow\)\(5x=10\)
\(\Leftrightarrow\)\(x=2\)
Vậy...
\(x^2-3x+1=x+x^2\)
\(\Leftrightarrow\)\(x^2-3x-x-x^2=-1\)
\(\Leftrightarrow\)\(-4x=-1\)
\(\Leftrightarrow\)\(x=\frac{1}{4}\)
Vậy...
mấy cái này bấm máy tính là đc òi. giải mất thời gian lắm :))

a) 4 ( x + 5 )( x + 6 )( x + 10 )( x + 12 ) = 3x2
Do x = 0 không là nghiệm pt nên chia 2 vế pt cho \(x^2\ne0\), ta được :
\(\frac{4}{x^2}\left(x^2+60+17x\right)\left(x^2+60+16x\right)=3\)
\(\Leftrightarrow4\left(x+\frac{60}{x}+17\right)\left(x+\frac{60}{x}+16\right)=3\)
Đến đây ta đặt \(x+\frac{60}{x}+16=t\left(1\right)\)
Ta được :
\(4t\left(t+1\right)=3\Leftrightarrow4t^2+4t-3=0\Leftrightarrow\left(2t+3\right)\left(2t-1\right)=0\)
Từ đó ta lắp vào ( 1 ) tính được x
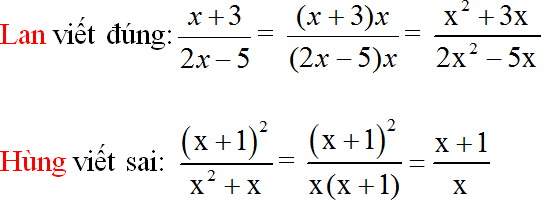
Lỗi sai: Khi chuyển vế hạng tử -x từ vế phải sang vế trái và hạng tử -6 từ vế trái sang vế phải không đổi dấu của hạng tử đó.
Sửa lại:
3x – 6 + x = 9 – x
⇔ 3x + x + x = 9 + 6
⇔ 5x = 15
⇔ x = 3.
Vậy phương trình có nghiệm duy nhất x = 3.