
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
$xy=-21=7.(-3)=(-7).3=3.(-7)=(-3).7=21.(-1)=(-21).1=(-1).21=1(-21)$
Do đó $(x,y)=(7,-3); (-7,3); (3,-7); (-3,7); (21,-1); (-21,1); (-1,21); (1,-21)$
b.
$(x+5)(y-3)=14=1.14=14.1=(-14)(-1)=(-1)(-14)=2.7=7.2=(-2)(-7)=(-7)(-2)$
Do đó:
$(x+5,y-3)=(1,14); (14,1); (-14,-1); (-1,-14); (2,7); (7,2); (-2,-7); (-7,-2)$
Đến đây thì đơn giản rồi.
c.
$x(y-2)=-19$, bạn làm tương tự
d. Tương tự

\(2y^2+x+x+y+1=x^2+2y^2+xy\)
\(\Leftrightarrow\left(2xy^2-2y^2\right)+\left(x-xy\right)+\left(x-x^2\right)=-1\)
\(\Leftrightarrow\left(x-1\right)\left(2y^2-y-x\right)=-1\)
\(\Leftrightarrow\left(x-1\right)\left(2y^2-y-x\right)=-1\)
\(\Rightarrow x-1;2y^2-y-x\LeftrightarrowƯ\left(-1\right)\)
[Nên x có thể là 1 số nguyên hoặc ko phải]
Đây cũng là kiểu bài làm quen tìm nghiệm lớp 8 nên mik sẽ loại từng TH :V
Ta sẽ có 2 TH
TH1:
\(\hept{\begin{cases}x-1=1\\2y^2-y-x=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\left(tm\right)\\y=1\left(tm\right)hay=-\frac{1}{2}\left(ktm\right)\end{cases}}}\)
TH2:
\(\hept{\begin{cases}x-1=-1\\2y^2-2y-x=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\left(tm\right)\\y=1\left(tm\right);y=-\frac{1}{2}\left(ktm\right)\end{cases}}}\)
Vậy nghiệm(x,y) là = (2;1);(0;1)
(Tùy thì có thể lập bảng GT nhưng k cắc nên trình bày ngu :D)


\(xy-\left(x+2y\right)=3\)
\(xy-x-2y=3\)
\(y\left(x-2\right)-x=3\)
\(y\left(x-2\right)-x+2=3+2\)
\(y\left(x-2\right)-\left(x-2\right)=5\)
\(\left(y-1\right)\left(x-2\right)=5\)
Ta có bảng sau:
| \(y-1\) | \(1\) | \(5\) | \(-1\) | \(-5\) |
| \(x-2\) | \(5\) | \(1\) | \(-5\) | \(-1\) |
| \(y\) | \(2\) | \(6\) | \(0\) | \(-4\) |
| \(x\) | \(7\) | \(3\) | \(-3\) | \(1\) |
Vậy các cặp \(\left(x;y\right)\) là \(\left(7;2\right);\left(3;6\right);\left(-3;0\right);\left(1;-4\right)\)
=>xy-x-2y=3
=>x(y-1)-2y+2=5
=>(x-2)(y-1)=5
=>\(\left(x-2;y-1\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(3;6\right);\left(7;3\right);\left(1;-4\right);\left(-3;0\right)\right\}\)

\(\left\{{}\begin{matrix}2xy+x+2y=5\\xy+3x-3y=5\end{matrix}\right.\)
\(\Rightarrow2xy+x+2y=xy+3x-3y\)
\(\Rightarrow2xy+x+2y-xy-3x+3y=0\)
\(\Rightarrow\left(2xy-xy\right)+\left(x-3x\right)+\left(2y+y\right)=0\)
\(\Rightarrow xy-2x+3y=0\)
\(\Rightarrow xy-2x+3y-6=-6\)
\(\Rightarrow x\left(y-2\right)+3\left(y-2\right)=-6\)
\(\Rightarrow\left(x+3\right)\left(y-2\right)=-6\)
Xét ước là xong,mấy câu kia tương tự



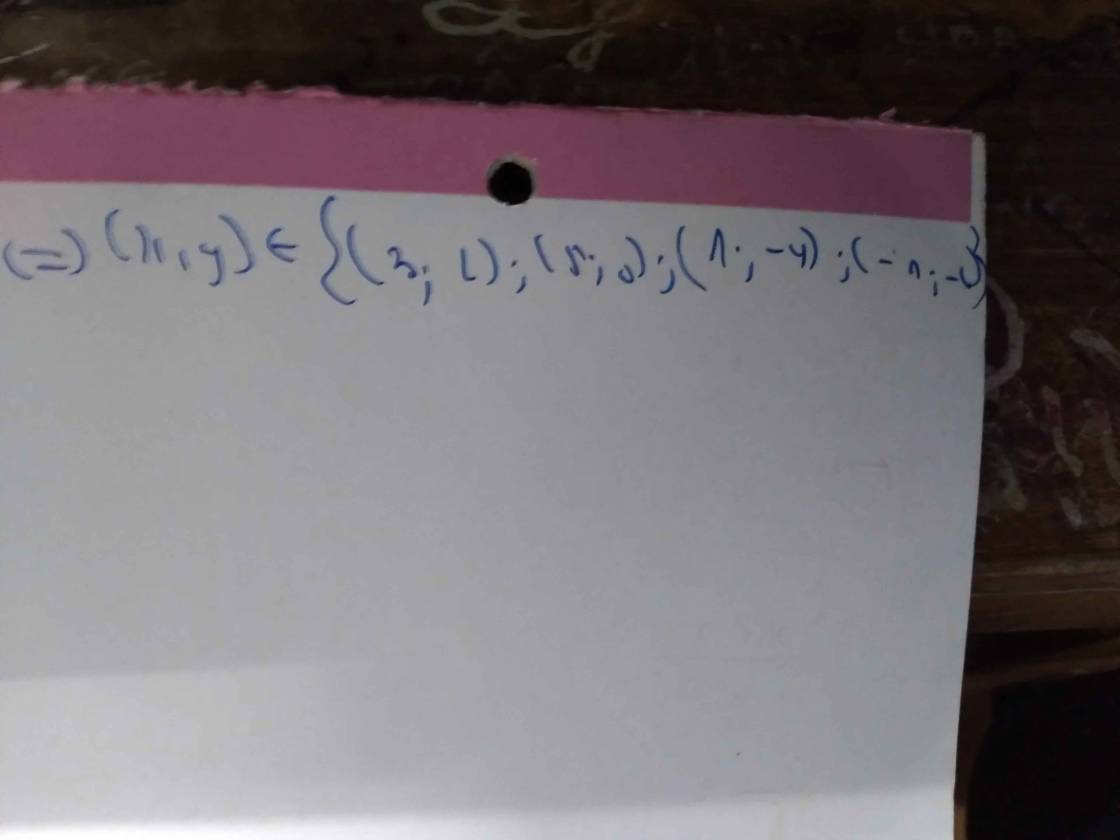
\(\left(2+x\right)\left(2y-1\right)=5\)
Ta có:\(5=1.5=5.1=\left(-1\right).\left(-5\right)=\left(-5\right).\left(-1\right)\)
Do đó ta có bảng sau:
Vậy cặp (x;y) TM là (-7;0)(-3;-2)(-1;3)(3;1)
Điều kiện là x,y nguyên nữa nha bn
Ta có bảng sau:
Vậy (x,y) \(\in\) {(-1;3);(3;1);(-3;-2);(-7;0)}