Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi cấp số nhân (un) cần tìm có công bội q, số hạng đầu tiên u1.
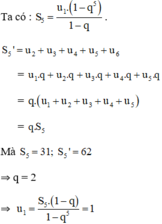
Vậy CSN (un) là: 1; 2; 4; 8; 16; 32.
Gọi 6 số hạng cấp số cộng là a,a+d,a+2d,...,a+5d. Suy ra
a+(a+d)+(a+2d)+...(a+4d)=5a+(1+2+3+4)d=5a+10d=31
a+d+(a+2d)+(a+3d)+...(a+5d)=5a+(1+2+3+4+5)d=5a+15d=62
Suy ra \(d=\dfrac{31}{5},a=-\dfrac{31}{5}\)
Chọn D
Cấp số nhân u n có số hạng đầu u 1 và công bội q
Do S n = 6 n - 1 nên q ≠ 1
Khi đó S n = u 1 ( 1 - q n ) 1 - q = 6 n - 1
Ta có : S 1 = u 1 ( 1 - q ) 1 - q ⇔ u 1 = 5
S 2 = u 1 1 - q 2 1 - q ⇔ q = 6
Vậy u 5 = u 1 . q 4 = 6480
Gọi 4 số cần tìm là \(a_1,a_2,a_3,a_4\). Theo đầu bài ta có hệ :
\(\begin{cases}a_2^2=a_1a_3\\2a_3=a_2+a_4\\a_1+a_4=14\\a_2+a_3=12\end{cases}\) \(\Leftrightarrow\begin{cases}2a_1q^2=a_1q+a_2+d\left(1\right)\\a_1+a_2+d=14\left(2\right)\\a_1q+a_1q^2=12\left(3\right)\\a_2+a_2+d=12\left(4\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2^2=a_1\left(a_2+d\right)\left(5\right)\\a_2+2d=14-a_1\\a_1=\frac{12}{q+q^2}\\d=12-2a_2\end{cases}\)
Giải hệ thống các phương trình ta có kết quả \(\left(2,4,8,12\right)\left(\frac{25}{2},\frac{15}{2}\frac{9}{2}\frac{3}{2}\right)\)
Tổng số lương của chuyên gia đó sau 10 năm là:
\(S=\dfrac{10\cdot\left[2\cdot240+10\cdot1.05\right]}{2}=2452.5\left(đồng\right)\)
a) \({u_1} = 5,\;\;{u_2} = 10,\;\;\;{u_3} = 15,\;\;{u_4} = 20,\;\;\;{u_5} = 25\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{5n}}{{5n - 1}} \)phụ thuộc vào n.
Suy ra dãy số \(\left( {{u_n}} \right)\) không phải là cấp số nhân.
b) \({u_1} = 5,\;\;{u_2} = 25,\;\;{u_3} = 125,\;\;\;{u_4} = 625,\;\;\;{u_5} = 3125\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{{5^n}}}{{{5^{n - 1}}}} = 5,\;\forall n \ge 2\).
Do đó dãy số \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 5\).
Số hạng tổng quát: \({u_n} = 5 \times {5^{n - 1}}= 5^{n}\).
c) \({u_1} = 1,\;\;\;{u_2} = 2,\;\;\;{u_3} = 6,\;\;\;{u_4} = 24,\;\;\;{u_5} = 120\).
có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = n\) phụ thuộc vào n, \(\forall n \in {N^*}\).
Suy ra dãy số \(\left( {{u_n}} \right)\) không phải là cấp số nhân.
d) \({u_1} = 1,\;\;{u_2} = 5,\;\;{u_3} = 25,\;\;\;{u_4} = 125,\;\;\;{u_5} = 625\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = 5,\;\forall n \ge 2\).
Do đó dãy số \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 5\).
Số hạng tổng quát: \({u_n} = {5^{n - 1}}\).
Chọn D
- Gọi u 1 , u 2 , . . . , u 7 là cấp số nhân cần tìm và q là công bội của cấp số nhân đó.
- Giả thiết ta có:
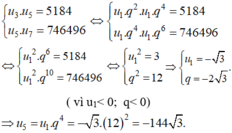
Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
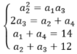
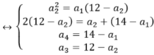
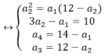
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D
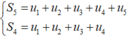
Giả sử có cấp số nhân: u1, u2, u3, u4, u5,u6.
Theo giả thiết ta có:
u1 + u2 + u3 + u4 + u5 = 31. (1)
và u2 + u3 + u4 + u5 + u6 = 62. (2)
Nhân hai vế của (1) với q, ta được: q.u1 + q.u2 + q.u3 +q. u4 +q. u5 = 31.q
hay u2 + u3 + u4 + u5 + u6 = 31q
Suy ra 62 = 31.q hay q = 2.
Ta có S5 = 31 =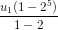
nên suy ra u1 = 1.
Vậy ta có cấp số nhân 1, 2, 4, 8, 16, 32.