Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ
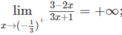
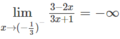
ta có x = −1/3 là tiệm cận đứng
Vì
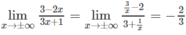
nên đường thẳng y = -2/3 là tiệm cận ngang.

Vì
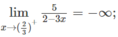
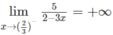
nên x = 2/3 là tiệm cận đứng.
Do
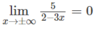
nên y = 0 là tiệm cận ngang.

Ta có:
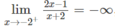
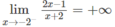
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
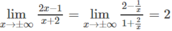
nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

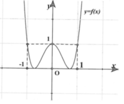
TXĐ: D = (- ∞ ; - 2 ) ∪ ( 2 ;4) ∪ (4; + ∞ )
Do
![]()
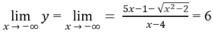
Cho nên đồ thị hàm số có hai tiệm cận ngang
y = 4 khi x ⇒ + ∞
y = 6 khi x ⇒ - ∞
Vì
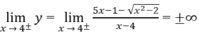
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.

- Cách tìm tiệm cận ngang:
+ Tính các giới hạn 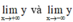
+ Nếu 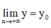 hoặc
hoặc 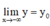 thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
- Cách tìm tiệm cận đứng:
Đường thẳng x = x o là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
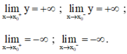

a) Ta có:
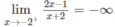
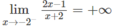
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
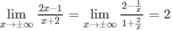
nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
b) Từ
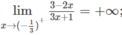
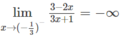
ta có x = −1/3 là tiệm cận đứng
Vì
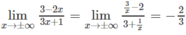
nên đường thẳng y = -2/3 là tiệm cận ngang.
c) Vì
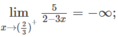
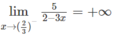
nên x = 2/3 là tiệm cận đứng.
Do
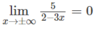
nên y = 0 là tiệm cận ngang.
d) Do
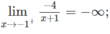
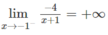
nên x = -1 là tiệm cận đứng.
Vì
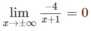
nên y = 0 là tiệm cận ngang.

Vì
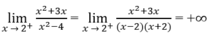
và
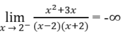
nên x = 2 là một tiệm cận đứng.
Do
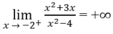
và
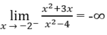
nên x = -2 là tiệm cận đứng thứ hai.
Ta lại có
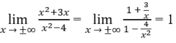
nên y = a là tiệm cận ngang.



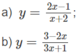
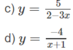
Do
nên x = -1 là tiệm cận đứng.
Vì
nên y = 0 là tiệm cận ngang.