Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ

Do
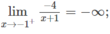
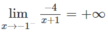
nên x = -1 là tiệm cận đứng.
Vì
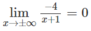
nên y = 0 là tiệm cận ngang.

Chọn C
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.

Từ
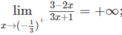
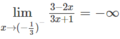
ta có x = −1/3 là tiệm cận đứng
Vì
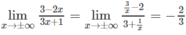
nên đường thẳng y = -2/3 là tiệm cận ngang.

- Cách tìm tiệm cận ngang:
+ Tính các giới hạn 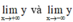
+ Nếu 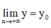 hoặc
hoặc 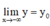 thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
- Cách tìm tiệm cận đứng:
Đường thẳng x = x o là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
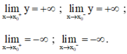

Vì
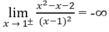
nên x = 1 là tiệm cận đứng.
Từ
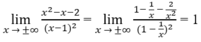
Suy ra y = 1 là tiệm cận ngang.



Ta có:
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.