
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
4

Các câu hỏi dưới đây có thể giống với câu hỏi trên

AV
9 tháng 7 2019
\(\frac{2n}{n-2}=\frac{2\left(n-2\right)+4}{n-2}=2+\frac{4}{n-2}\)(ĐK:n\(\ne2\))
để biểu thức nhận gái trị nguyên thì 4\(⋮\)(n-2)
=> (n-2) là ước của 4 mà Ư\(_{\left(4\right)}\)=\(\pm1;\pm2;\pm4\)
=>n-2=1 =>n=3 (tm)
n-2=-1 =>n=1 (tm)
n-2=2 =>n=4 (tm)
n-2=-2 =>n=0 (tm)
n-2=4=>n=6 (tm)
n-2=-4=>n=-2 (tm)

CM
10 tháng 3 2017
Đáp án cần chọn là: C
Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z
Vì n∈Z nên để C∈Z thì 2n + 1∈U(11) = {±1;±11}
Ta có bảng
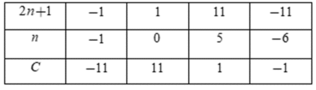
Vì C∈N nên ta chỉ nhận các giá trị n = 0;n = 5

CM
26 tháng 1 2017
Đáp án cần chọn là: B
Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z
Vì n∈Z nên để C∈Z thì 3n − 2∈U(12) = {±1;±2;±3;±4;±6;±12}
Ta có bảng:
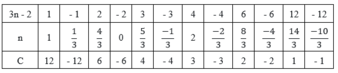
Vì C∈N và n∈Z nên ta chỉ nhận các giá trị n = 1;n = 2

\(\frac{n}{n-4}\)nhận giá trị nguyên <=> n\(⋮\)n - 4
< => ( n - 4 ) + 4 \(⋮\) n - 4
<=> 4 \(⋮\) n - 4
<=> n - 4 \(\in\)Ư ( 4 )
<=> n - 4 \(\in\){ 1;2;4;-1;-2;-4 }
<=> n \(\in\){ 5;6;8;3;2;0 }
vậy ....
Để biểu thức đạt giá trị nguyên thì:
\(\frac{n}{n-4}\in Z\Rightarrow n⋮n-4\)
Xét từng th -> giải.