
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giả sử hai số cần tìm là z1 và z2.
Ta có: z1 + z2 = 3; z1. z2 = 4
Rõ ràng, z1, z2 là các nghiệm của phương trình:
(z – z1)(z – z2) = 0 hay z2 – (z1 + z2)z + z1. z2 = 0
Vậy z1, z2 là các nghiệm của phương trình: z2 – 3z + 4 = 0
Phương trình có Δ = 9 – 16 = -7
Vậy hai số phức cần tìm là: z1=3+i√72,z2=3−i√72

Hai số phức có tổng bằng 3, tích bằng 4 là nghiệm của phương trình:
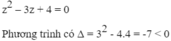
⇒ Phương trình có hai nghiệm: 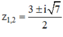
Vậy hai số cần tìm là 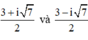

Để tìm số tự nhiên lớn nhất thỏa mãn điều kiện trên, chúng ta cần tìm số tự nhiên lớn nhất mà khi chia cho cả 428 và 708 đều có số dư.
Để làm điều này, chúng ta có thể sử dụng thuật toán Euclid mở rộng. Bắt đầu với hai số 428 và 708, ta thực hiện các bước sau:
1. Tìm ước số chung lớn nhất (GCD) của 428 và 708 bằng cách sử dụng thuật toán Euclid:
- 708 = 428 * 1 + 280
- 428 = 280 * 1 + 148
- 280 = 148 * 1 + 132
- 148 = 132 * 1 + 16
- 132 = 16 * 8 + 4
- 16 = 4 * 4 + 0
GCD của 428 và 708 là 4.
2. Sau đó, chúng ta tìm bội số chung nhỏ nhất (LCM) của 428 và 708 bằng cách sử dụng công thức:
LCM = (428 * 708) / GCD
LCM = (428 * 708) / 4 = 151,704
Vậy số tự nhiên lớn nhất mà khi chia cho cả 428 và 708 đều có số dư là 151,704.

Chọn: C
![]()
![]()
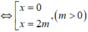
Tọa độ hai điểm cực trị: A 0 ; 3 m 3 , B 2 m ; - m 3
![]()
Ta có: y = y ' . 1 3 x - m 3 - 2 m x + 3 m 3
⇒ Phương trình đường thẳng đi qua hai điểm cực trị là:
![]()
⇒ d O ; A B = 3 m 3 4 m 4 + 1
Diện tích tam giác OAB là;
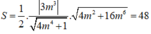
![]()
Tổng hai giá trị của m là: -2 + 2 = 0