Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt 7p+1=n3(n>2)(n\(\inℕ\))
=>7p=(n-1)n(n+1)=(n-1)(n2+n+1) *
Xét p=2=>loại
Xét p>2=>p là số nguyên tố lẻ
Mà n2+n+1=n(n+1)+1 luôn lẻ
Từ * ta có \(\hept{\begin{cases}n-1=7\\n^2+n+1=p\end{cases}}\Leftrightarrow\hept{\begin{cases}n=8\\p=31\end{cases}}\)
(THOẢ MÃN)

1.Với a = 2 ta có 2a + 1 = 5 không thích hợp
Với a ≠ 2 do a là số nguyên tố nên a lẽ
Vậy 2a + 1 là lập phương của một số lẽ nghĩa là
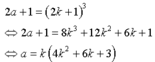
Từ đó k là ước của a. Do k là số nguyên tố nên k = 1 hoặc k = a
-Nếu k = 1 thì 2a + 1 = (2.1 + 1)3 suy ra a = 13 thớch hợp
- Nếu a = k từ a = a(4a2 + 6a + 3) do a là nguyên tố nên suy ra
1 = 4a2 + 6a + 3 không có số nguyên tố a nào thoả món phương trỡnh này Vì vế phải luụn lớn hơn 1
Vậy a = 13
2.Giả sử

13 và p là các số nguyên tố , mà n – 1 > 1 và n2 + n + 1 > 1
Nên n – 1 = 13 hoặc n – 1 = p
- Với n – 1 =13 thì n = 14 khi đó 13p = n3 – 1 = 2743 suy ta p = 211 là số nguyên tố
- Với n – 1 = p thi n2 + n + 1 = 13 suy ra n = 3 . Khi đó p = 2 là số nguyên tố
Vậy p = 2, p = 211 thì 13p + 1 là lập phương của một số tự nhiên

xin lỗi tớ nhầm
Đặt 2p + 1 = n³ với n là số tự nhiên
Cách giải: phân tích ra thừa số
Dùng tính chất : Số nguyên tố có 2 ước là 1 và chính nó.
Giải:
♣ Ta thấy p = 2 thì 2p + 1 = 5 không thỏa = n³
♣ Nếu p > 2 => p lẻ (Do Số nguyên tố chẵn duy nhất là 2 )
Mặt khác : 2p + 1 là 1 số lẻ => n³ là một số lẻ => n là một số lẻ
=> 2p + 1 = (2k + 1)³ ( với n = 2k + 1 )
<=> 2p + 1 = 8k³ + 12k² + 6k + 1
<=> p = k(4k² + 6k + 3)
=> p chia hết cho k
=> k là ước số của số nguyên tố p.
Do p là số nguyên tố nên k = 1 hoặc k = p
♫ Khi k = 1
=> p = (4.1² + 6.1 + 3) = 13 (nhận)
♫ Khi k = p
=> (4k² + 6k + 3) = (4p² + 6p + 3) = 1
Do p > 2 => (4p² + 6p + 3) > 2 > 1
=> không có giá trị p nào thỏa.
Đáp số : p = 13

- Giả sử 13. p + 1 = n3 \(\left(n\inℕ\right)\)
Vì \(p\ge2\) nên \(n\ge3\)
Ta có 13p = n3 - 1 = ( n - 1 ) x ( n2 + n + 1 )
Do 13 và p là các số nguyên tố và n2 + n + 1 > n - 1 > 1 nên n - 1 = 13 hoặc n - 1 = p
- Với n - 1 = 13 thì n =14. Khi đó 13p = n3 - 1 = 2743 nên p = 211 là số nguyên tố
- Với n - 1 = p thì n2 + n + 1 = 13 nên n = 3 khi đó p = 2 là số nguyên tố
Vậy \(p\in\left\{2;211\right\}\)
Cbht
lập phương không phải bình phương
\(7p+1=n^3\)(n∈N)
\(7p=n^3-1=\left(n-1\right)\left(n^2+n+1\right)\)
Vì p là SNT nên ta có 4 TH:
TH1: n-1=p⇒\(n^2+n+1=7\) vì n là STN nên thử các TH thấy n=2
⇒p=2-1=1(vô lí vì 1 ko là SNT)
TH2: n-1=7⇒n=8⇒\(p=\frac{8^3-1}{7}=73\) là số nguyên tố(thỏa mãn)
TH3: n-1=1⇒n=2⇒\(p=\frac{2^3-1}{7}=1\) ko là số nguyên tố(loại)
TH4: n-1=7p ; n2+n+1=1 thì vô lí do n2+n+1>n
Vậy p=73