
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bất phương trình x2-3x+2 ≤ 0 ⇔ 1 ≤ x ≤ 2
Bất phương trình mx2+(m+1) x+m+1 ≥ 0
![]()
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 , 1 ≤ x ≤ 2
Có f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.

Giải bất phương trình x2- 3x+ 2≤ 0 ta được 1≤x≤2.
Bất phương trình mx2+ (m+ 1) x+ m+1≥0
⇔ m ( x 2 + x + 1 ) ≥ - x - 2 ⇔ m ≥ - x - 2 x 2 + x + 1
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 với 1≤ x≤ 2
Có đạo hàm f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 , ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.

\(\Leftrightarrow m\left(\sqrt{x^2+2}-1\right)=x\)
\(\Leftrightarrow m=\dfrac{x}{\sqrt{x^2+2}-1}\)
Xét hàm \(f\left(x\right)=\dfrac{x}{\sqrt{x^2+2}-1}\)
\(f'\left(x\right)=\dfrac{2-\sqrt{x^2+2}}{\sqrt{x^2+2}\left(\sqrt{x^2+2}-1\right)^2}\)
\(f'\left(x\right)=0\Rightarrow x=\pm\sqrt{2}\)
\(f\left(\sqrt{2}\right)=\sqrt{2}\) ; \(f\left(-\sqrt{2}\right)=-\sqrt{2}\) ; \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=1\) ; \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-1\)
BBT:
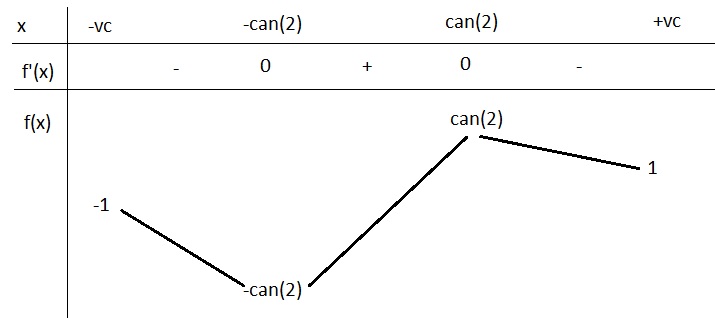
Từ BBT ta thấy pt có 2 nghiệm pb khi \(\left[{}\begin{matrix}-\sqrt{2}< m< -1\\1< m< \sqrt{2}\end{matrix}\right.\)

Để pt có nghiệm thì
\(1+x\ne0\) và \(8-x\ne0\)
\(\Rightarrow x\ne-1\) và \(x\ne8\)
\(\sqrt{1+x} +\sqrt{8-x}+\sqrt{\left(1+x\right)\left(8-x\right)}=m\)
( mk viết thiếu đề)



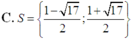

\(2^{x-2}=8^{100}\)
=>\(2^{x-2}=2^{300}\)
=>x-2=300
=>x=302