Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$


Diện tích đáy lăng trụ là:
\(S=\dfrac{1}{2}\cdot2x=x\left(cm^2\right)\)
\(V=S\cdot h\)
=>x=V/h=3(cm)

Ta có 3x^2-x+1=3x^2+2x-3x-2+3=(3x-2)(x-1)+3
D có giá trị nguyên\(\) khi 3\(⋮\)(3x+2)\(\Leftrightarrow\)3x+2 là ước của 3\(\Leftrightarrow\)3x+2\(\in\){-3;-1;1;3} suy ra x\(\in\){-5/3;-1;-1/3;1/3}mà x nguyên nên ta tìm được x=-1

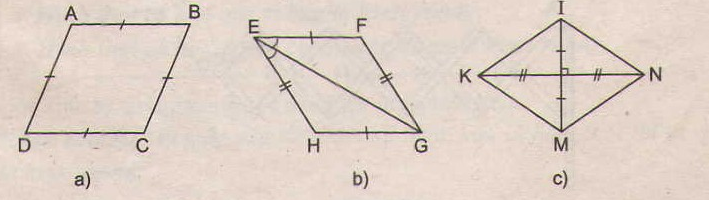
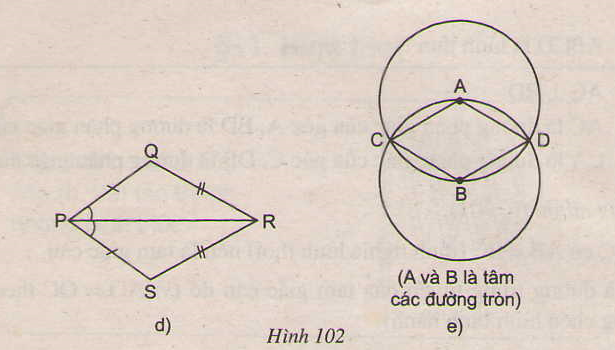
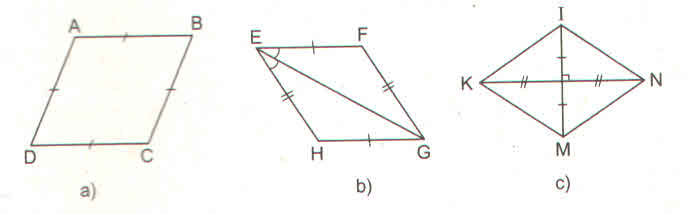
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.

điều kiện: \(x\ne\pm3\)
A = \(\frac{3\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\frac{x+3}{\left(x+3\right)\left(x-3\right)}+\frac{18}{\left(x-3\right)\left(x+3\right)}\)
= \(\frac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\frac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
= \(\frac{4}{x-3}\)
Với x = 1 thì A = \(\frac{4}{1-3}=-2\)
a, ĐKXĐ : x+3 khác 0 ; x-3 khác 0 ; x^2-9 khác 0 <=> x khác -3 và 3
b, A = 3.(x-3)+x+3+18/(x-3).(x+3) = 4x+12/(x+3).(x-3) = 4.(x+3)/(x+3).(x-3) = 4/x-3
c, Khi x =1 thì A = 4/1-3 = -2
k mk nha

a) \(x\ne2\) ; \(x\ne-2\)
b) Ta có
\(C=\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}=\frac{x^3}{\left(x-2\right)\left(x+2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3-x.\left(x+2\right)-2.\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\frac{x^2.\left(x-1\right)-4.\left(x-1\right)}{x^2-4}\)
\(=\frac{\left(x-1\right)\left(x^2-4\right)}{x^2-4}=x-1\)
Để C = 0 thì x-1 = 0 =>>> x=1(tm)
c) Để C nhận giá trị dương thì C thuộc Z+ = >>>>>>>> \(x-1\ge0\)=>>> \(x\ge1\)
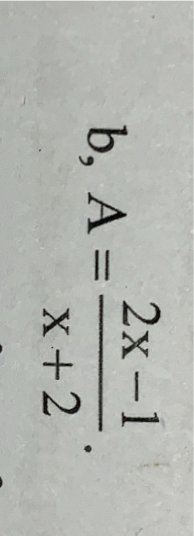









\(A=\dfrac{2x-1}{x+2}\)
\(\Rightarrow A=\dfrac{2x+4-5}{x+2}\)
\(\Rightarrow A=\dfrac{2\left(x+2\right)-5}{x+2}\)
\(\Rightarrow A=\dfrac{2\left(x+2\right)}{x+2}-\dfrac{5}{x+2}\)
\(\Rightarrow A=2-\dfrac{5}{x+2}\)
\( Để.A\in Z.mà.2\in Z\Rightarrow\dfrac{5}{x+2}\in Z\Rightarrow5⋮\left(x+2\right)\Rightarrow x+2\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Ta có bảng:
Vậy \(x\in\left\{-3;-7;-1;3\right\}\)
Cho mình hỏi là tại sao ở trên là 2x-1 mà ở dưới lại là 2x+4-5