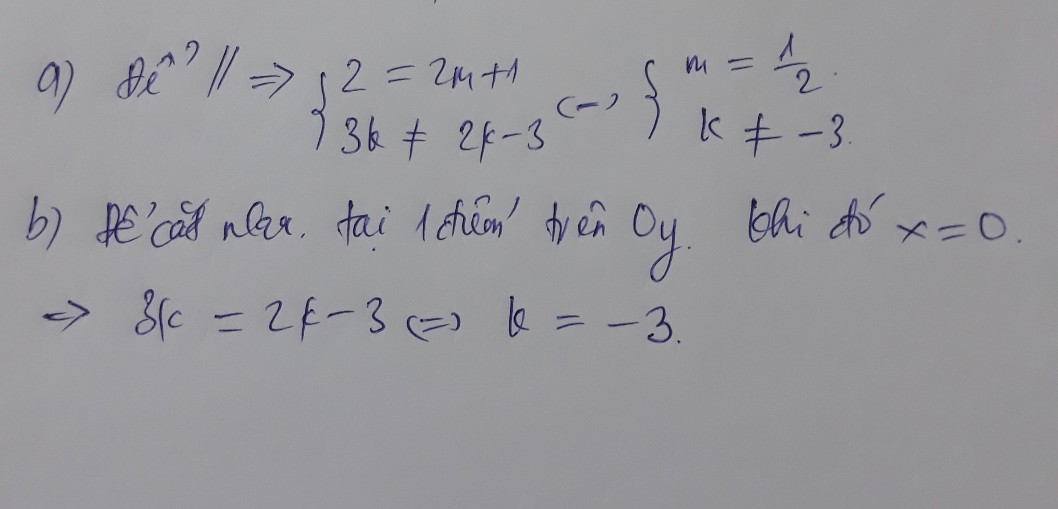Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Đk: (D) //(D'') là:
\(m=3m-4\)
<=> \(2m=4\)<=> m = 2.
b/ ĐK: ( D) cắt (D'') là:
\(m\ne3m-4\Leftrightarrow m\ne2\)
c) ĐK để (D) vuông (D''0 là:
\(m.\left(3m-4\right)=-1\)
<=> \(3m^2-4m+1=0\)
<=> m =1 hoặc m=1/3

a, cắt : a khác a'
b, b= b'; a khác a'
c, a=a' ; b khác b'
d, a*a'= -1
e, a= a' ;b= b'

a) Hàm số \(y=2x+3k\) có các hệ số \(a=2,b=3k\)
Hàm số \(y=\left(2m+1\right)x+2k-3\) có các hệ số \(a'=2m+1,b'=2k-3\)
Hai hàm số đã cho là hàm số bậc nhất nên \(2m+1\ne0\)
\(\Leftrightarrow m\ne-\frac{1}{2}\)
Hai đường thẳng song song với nhau khi \(a=a'\) và \(b\ne b'\) tức là:
\(2=2m+1\) và \(3k\ne2k-3\)
Kết hợp với điều kiện trên ta có: \(m=\frac{1}{2}.k\ne-3\)
b) Hai đường thẳng song song:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k\ne2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k\ne-3\end{cases}}\)
c) Hai đường thẳng trùng nhau:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k=2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k=-3\end{cases}}\)

1) Không thể trùng nhau vì b \(\ne\)b'
2)
a) song song khi \(\int^{m-1=3}_{2\ne-1}\Rightarrow m=4\)
b) cắt nhau a\(\ne\)a' => m\(\ne\)4
c) vuông góc với nhau khi a.a' =-1 =>3(m-1) =-1 => m-1 =-1/3 => m = 1 - 1/3 =2/3