Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Dễ thấy \(x^2\)luôn dương vậy để A dương thì \(4x\ge0\)
\(\Leftrightarrow x\ge0\)
b) \(B=\left(x-3\right)\left(x+7\right)\)dương khi :
TH1: \(\hept{\begin{cases}x-3>0\\x+7>0\end{cases}\Rightarrow\hept{\begin{cases}x>3\\x>-7\end{cases}\Rightarrow}x>3}\)
TH2: \(\hept{\begin{cases}x-3< 0\\x+7< 0\end{cases}\Rightarrow\hept{\begin{cases}x< 3\\x< -7\end{cases}\Rightarrow}x< -7}\)
c) Tương tự câu b)

a) Ta có ; \(x^2\ge0\forall x\in R\)
Nên A dương khi 4x \(\ge0\forall x\in R\)
=> \(x\ge0\)
Vậy A dương khi \(x\ge0\)

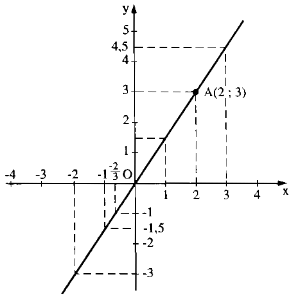
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) =0
b)\(y=-1\Rightarrow x=\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
\(y=0\Rightarrow x=\dfrac{0}{1,5}=0\)
\(y=4,5\Rightarrow x=\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.

a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) = 0
b)y=−1⇒x=\(\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
b)y=0⇒x==\(\dfrac{0}{1,5}=0\)
y=4,5⇒x=\(\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0

Bài 1:
a: \(\left(2x-1\right)^4=16\)
=>2x-1=2 hoặc 2x-1=-2
=>2x=3 hoặc 2x=-1
=>x=3/2 hoặc x=-1/2
b: \(\left(2x-y+7\right)^{2012}+\left|x-3\right|^{2013}< =0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y+7=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2x+7=y=2\cdot3+7=13\end{matrix}\right.\)
c: \(10800=2^4\cdot3^3\cdot5^2\)
mà \(2^{x+2}\cdot3^{x+1}\cdot5^x=10800\)
nên \(\left\{{}\begin{matrix}x+2=4\\x+1=3\\x=2\end{matrix}\right.\Leftrightarrow x=2\)

2.
a/\(A=5-I2x-1I\)
Ta thấy: \(I2x-1I\ge0,\forall x\)
nên\(5-I2x-1I\le5\)
\(A=5\)
\(\Leftrightarrow5-I2x-1I=5\)
\(\Leftrightarrow I2x-1I=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy GTLN của \(A=5\Leftrightarrow x=\frac{1}{2}\)
b/\(B=\frac{1}{Ix-2I+3}\)
Ta thấy : \(Ix-2I\ge0,\forall x\)
nên \(Ix-2I+3\ge3,\forall x\)
\(\Rightarrow B=\frac{1}{Ix-2I+3}\le\frac{1}{3}\)
\(B=\frac{1}{3}\)
\(\Leftrightarrow B=\frac{1}{Ix-2I+3}=\frac{1}{3}\)
\(\Leftrightarrow Ix-2I+3=3\)
\(\Leftrightarrow Ix-2I=0\)
\(\Leftrightarrow x=2\)
Vậy GTLN của\(A=\frac{1}{3}\Leftrightarrow x=2\)
a) Để \(\left(x+1\right)^2\left(y-6\right)=0\)
thì \(\orbr{\begin{cases}x+1=0\\y^2-6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\y=\sqrt{6}\end{cases}}}\)
b) \(x^2-12x+7>7\Leftrightarrow x^2-12x>0\)
\(\Leftrightarrow x\left(x-12\right)>0\)
\(\Leftrightarrow\orbr{\begin{cases}\hept{\begin{cases}x>0\\x-12>0\end{cases}}\\\hept{\begin{cases}x< 0\\x-12< 0\end{cases}}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>12\\x< 0\end{cases}}\)