K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 6 2016
a) Tam giác ABC vuông tại A nên có +
= 900
Hay ,
phụ nhau, tam giác AHB vuông tại H nên có
+
= 900
hay ,
phụ nhau. Tam giác AHC vuông tại H nên có
+
= 900
hay ,
phụ nhau.
b) Ta có +
= 900
+
= 900
=> =
+
= 900
và +
= 900
=> =
13 tháng 6 2016
A) các cặp góc phụ nhau : góc BAH và góc ABH ; góc HAC và góc HCA; góc ABC và góc ACB
B) các cặp góc nhọn bằng nhau : góc HCA và góc HBA ; góc HAC và góc HAB; góc ACH và góc ABH
TN
24 tháng 5 2016
a. các cặp góc phụ nhau là:
góc ABC và góc ACB
góc ABH và góc BAH
góc ACH và góc CAH
b. các cặp góc nhọn bằng nhau là:
góc ABC= góc CAH(vì cùng phụ góc ACH)
góc BAH= góc ACB(vì cùng phụ góc ABH)
24 tháng 5 2016
a) Tam giác ABC vuông tại A nên có +
= 900
Hay ,
phụ nhau, tam giác AHB vuông tại H nên có
+
= 900
hay ,
phụ nhau. Tam giác AHC vuông tại H nên có
+
= 900
hay ,
phụ nhau.
b)
Ta có +
= 900
+
= 900
=> =
+
= 900
và +
= 900
=> =
29 tháng 1 2021
a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)
MY
12 tháng 11 2019
các cặp tam giác bằng nhau là
ACH=CHK
ABH=HBK
ABC=BCK
ACK=ABK(nó chỉ đúng khi góc B và góc C của tam giác ABC có số đo góc bằng nhau)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
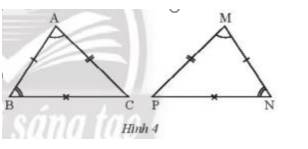
\( \Rightarrow \Delta{ABC}=\Delta{MNP}\) do có các cặp góc và cạnh tương ứng bằng nhau.
Các cặp góc bằng nhau là: \(\widehat A = \widehat M\); \(\widehat B = \widehat N\);\(\widehat C = \widehat P\)
Các cặp cạnh bằng nhau là: \(AB = MN; AC = MP; BC = PN\)
TG
18 tháng 9 2023
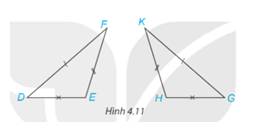
Các cặp cạnh tương ứng : FE = KH , ED = HG , DF = GK
Các góc tương ứng : góc F = góc K, góc E = góc H, góc D = góc G
Kí hiệu bằng nhau của tam giác đó : ΔDFE=ΔGKH
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Ta có: Các cặp góc tương ứng là: \(\widehat E = \widehat H;\widehat D = \widehat G;\widehat F = \widehat K\)
Các cặp cạnh tương ứng là:\(ED=HG;EF=HK;DF=GK\)
CT
16 tháng 11 2018
â, góc AHC , góc AHB ; còn câu b , mk đang suy nghĩ CM , bn kb vs mk rùi tụi mk bàn bạc nhé !
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
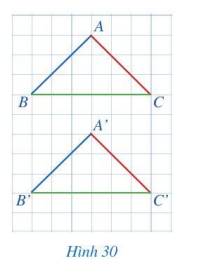
a) AB = A’B’; BC = B’C’; CA = C’A’.
A = A’; B = B’; C = C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.