Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Lấy $M(x,y)\in (d)$. $M'(x',y')=T_{\overrightarrow{v}}(M)$
\(\left\{\begin{matrix} x'-x=2\\ y'-y=-1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=x'-2\\ y=y'+1\end{matrix}\right.\)
Ảnh của $d$ qua phép tịnh tiến theo vecto $\overrightarrow{v}$ có dạng:
$3(x'-2)-2(y'+1)+1=0$
$\Leftrightarrow 3x'-2y'-7=0$
Câu 2:
$M(x,y)$ là 1 điểm thuộc đường tròn $(C)$.
Lấy $M'(x',y')$ là 1 điểm thuộc $(C')$ là ảnh của $(C)$ qua $\overrightarrow{v}$
Khi đó, $M'=T_{\overrightarrow{v}}(M)
\(\Rightarrow \left\{\begin{matrix} x'-x=-3\\ y'-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=x'+3\\ y=y'-5\end{matrix}\right.\)
PTĐTr $(C')$ có dạng:
$(x'+3)^2+(y'-5)^2-4(x'+3)+6(y'-5)+5=0$
$\Leftrightarrow x'^2+y'^2+2x'-4y'-3=0$

Tọa độ A' là:
\(\left\{{}\begin{matrix}x=-2+3=1\\y=3-2=1\end{matrix}\right.\)
Lấy B(0;-2) thuộc (d)
=>Tọa độ B' là: \(\left\{{}\begin{matrix}x=0+3=3\\y=-2-2=-4\end{matrix}\right.\)
Thay x=3 và y=-4 vào (d'): 4x+3y+c=0, ta được:
c+12-12=0
=>c=0
(C): (x-3)^2+(y-1)^2=9
=>R=3 và I(3;1)
=>I'(5;-5)
=>(C'): (x-5)^2+(y+5)^2=9

(C) có \(\left\{{}\begin{matrix}I\left(2;3\right)\\R=3\end{matrix}\right.\)
\(T_{\overrightarrow{v}}\left(I\right)=I'\left(x',y'\right)\)\(\Rightarrow\left\{{}\begin{matrix}x'=x+a=2+\left(-1\right)=1\\y'=y+a=3+2=5\end{matrix}\right.\Rightarrow I'\left(1,5\right)\)
\(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\) có \(\left\{{}\begin{matrix}I'\left(1,5\right)\\R=3\end{matrix}\right.\)
\(\Rightarrow\) \(\left(C'\right):\left(x-1\right)^2+\left(y-5\right)^2=3\)

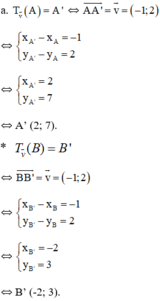
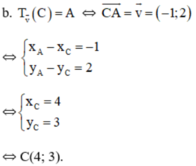
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
(C) có \(\left\{{}\begin{matrix}I\left(4,0\right)\\R=4\end{matrix}\right.\)
\(T_{\overrightarrow{v}}\left(I\right)=I'(x',y')\Rightarrow\left\{{}\begin{matrix}x'=x+a=4+3=7\\y'=y+a=0+\left(-1\right)=-1\end{matrix}\right.\) \(\Rightarrow I'\left(7,-1\right)\)
\(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\) có tâm \(I'\left(7,-1\right)R=4\)
\(\Rightarrow\left(C'\right):\left(x-7\right)^2+\left(y+1\right)^2=4\)