TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
29 tháng 12 2018
Lời giải:
\(A=\left\{x\in \mathbb{N}|x-2\vdots 5, x< 200\right\}\)
\(x< 200\Rightarrow x-2< 198\)
Vì $x\in\mathbb{N}$; $x-2\vdots 5$ nên \(x-2\) nhân các giá trị từ $0,5,...,195$
\(\Rightarrow x\) có thể nhận các giá trị từ $02,7,..,197$
Vậy \(A=\left\{2;7;...;197\right\}\). Tập này có \(\frac{197-2}{5}+1=40\) phần tử.
10 tháng 9 2020
BÀI GIẢI
VÌ A là số tự nhiên chia hết cho 9 nên tổng các chữ số của A phải chia hết cho 9 suy ra số A có dạng đơn giản nhất là 1000...08 (với chữ số 0 xuất hiện 2018 lần)
B là tổng các chữ số của A nên +
C là tổng các chữ số của B nên
D là tổng các chữ số của C nên
đáp án là 9
NH
0
NH
3
HT
7 tháng 11 2016
1) Tổng quát ta có A = \(\sum\limits^{k=1}_n\frac{1}{2^k}\) khi đó \(\lim\limits_{x\rightarrow+\infty}A=0\)
22 tháng 11 2016
1, tổng cấp số nhân lùi vô hạn \(A=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1\)
AH
Akai Haruma
Giáo viên
6 tháng 7 2019
Lời giải:
Ta có:
\(y=\frac{k\sin x+1}{\cos x+2}\Rightarrow y\cos x+2y=k\sin x+1\)
\(\Leftrightarrow 2y-1=k\sin x-y\cos x\)
Theo BĐT Bunhiacopxky:
\((2y-1)^2=(k\sin x-y\cos x)^2\leq (k^2+y^2)(\sin ^2x+\cos ^2x)=k^2+y^2\)
\(\Leftrightarrow 4y^2-4y+1\leq k^2+y^2\)
\(\Leftrightarrow 3y^2-4y+1\leq k^2\)
\(\Leftrightarrow 3(y-\frac{2}{3})^2\leq k^2+\frac{1}{3}\)
\(\Leftrightarrow \frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\leq y\leq \frac{2}{3}+\sqrt{\frac{3k^2+1}{9}}\)
\(\Rightarrow y_{\min}=\frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\)
Để \(y_{\min}< -1\Leftrightarrow \sqrt{\frac{3k^2+1}{9}}>\frac{5}{3}\Leftrightarrow k^2>8\Leftrightarrow \left[\begin{matrix} k>2\sqrt{2}\\ k<-2\sqrt{2}\end{matrix}\right.\)
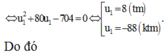
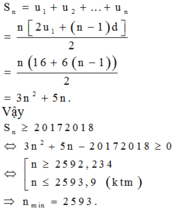
Đề bài yêu cầu gì?