Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình đường tròn (C) có dạng:
x2 + y2 -2ax – 2by + c= 0 ( a2+ b2 –c > 0)
Do 3 điểm A; B; C thuộc (C) nên
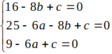
=>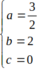
Vậy bán kính R= a 2 + b 2 - c 2 = 6 , 25
Chọn C.

a.
Gọi phương trình đường tròn (C) có dạng:
\(x^2+y^2-ax-by+c=0\)
Do A;B;C thuộc (C) nên: \(\left\{{}\begin{matrix}0+16-0.a-4b+c=0\\9+16-3a-4b+c=0\\9+0-3a-0.b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4b+c=-16\\-3a-4b+c=-25\\-3a+c=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=4\\c=0\end{matrix}\right.\)
Hay pt (C) có dạng: \(x^2+y^2-3x-4y=0\)
b.
Đường tròn (C) tiếp xúc (d) nên có bán kính \(R=d\left(C;d\right)=\dfrac{\left|3.3+0.4-5\right|}{\sqrt{3^2+4^2}}=\dfrac{4}{5}\)
Phương trình: \(\left(x-3\right)^2+y^2=\dfrac{16}{25}\)

Phương trình đường tròn (C) có dạng:
x2 + y2 -2ax – 2by + c= 0 ( a2+ b2 –c > 0)
Do 3 điểm A; B; C thuộc (C) nên
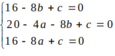
⇒
Vậy tâm I( 1;1)
Chọn D.


a.
\(\overrightarrow{AB}=\left(-6;3\right)\Rightarrow AB=\sqrt{\left(-6\right)^2+3^2}=3\sqrt{5}\)
Đường tròn (C) tâm A và đi qua B có bán kính \(R=AB=3\sqrt{5}\)
Phương trình:
\(\left(x-3\right)^2+\left(y-1\right)^2=45\)
b.
Gọi M là trung điểm AB \(\Rightarrow M\left(0;\dfrac{5}{2}\right)\)
Đường tròn đường kính AB có tâm M và bán kính \(R=\dfrac{AB}{2}=\dfrac{3\sqrt{5}}{2}\)
Phương trình:
\(x^2+\left(y-\dfrac{5}{2}\right)^2=\dfrac{45}{4}\)

Ta có :
\(\overrightarrow{AB}\) = (-3;-4)
\(\Rightarrow\overrightarrow{n}=\left(4;-3\right)\) là vectơ pháp tuyến của đường thẳng AB
Vậy phương trình đường thẳng AB là :
4x - 3(y-4) = 0
hay 4x - 3y = -4
Câu b tương tự

Gọi \(M\left(x;y\right)\Rightarrow\left(x+3\right)^2+\left(y+4\right)^2=1\)
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;2-y\right)\\\overrightarrow{MB}=\left(-2-x;1-y\right)\\\overrightarrow{MC}=\left(3-x;4-y\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\left(2-3x;7-3y\right)\)
\(T^2=\left(3x-2\right)^2+\left(3y-7\right)^2\)
Đặt \(\left(x+3;y+4\right)=\left(a;b\right)\Rightarrow a^2+b^2=1\)
\(T^2=\left(3a-11\right)^2+\left(3b-19\right)^2\)
\(T^2=9\left(a^2+b^2\right)-66a-114b+482=491-6\left(11a+19b\right)\)
Ta lại có:
\(\left(11a+19b\right)^2\le\left(11^2+19^2\right)\left(a^2+b^2\right)=482\)
\(\Rightarrow11a+19b\ge-\sqrt{482}\)
\(\Rightarrow T^2\le491+6\sqrt{482}\)
\(\Rightarrow T\le\sqrt{491+6\sqrt{482}}\)
Số liệu bài toán cho xấu 1 cách phi lý và vô nghĩa
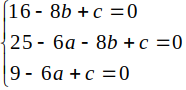
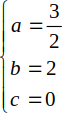
\(AB^2=AC^2+BC^2-2.AC.BC.\cos C\Rightarrow\sin C=...\)
\(\dfrac{BC}{\sin A}=\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}=2R\)
Mấu chốt là bạn phải tìm được độ dài các cạnh, độ dài các cạnh :công thức trong SGK