Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quan sát Hình 79, ta thấy bóng của các đường thẳng song song là các đường thẳng song song.
Bóng của các đường thẳng song song là các đường thằng song song

a) Quan sát Hình 78, ta thấy các điểm A’, B’, C’ thẳng hàng và điểm B’ nằm giữa hai điểm A’, C’.
b) Bóng nắng của thanh lan can là đường thẳng.

Gọi O là trung điểm của AC
Hình bình hành ACC'A' có: OO' // AA'
Vì O thuộc (ABCD)
Do đó: O là ảnh của O'.


Ta có: B là ảnh của A' lên (ABCD)
Có: D'C // A'B nên C là ảnh của D' lên (ABCD)
Từ C' kẻ C'E // CD' // A'B. Suy ra E là ảnh của C' lên (ABCD).
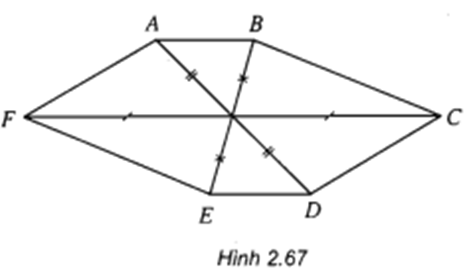
Vậy tam giác BCE là ảnh của tam giác A'C'D' qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A'B.

Bài giải
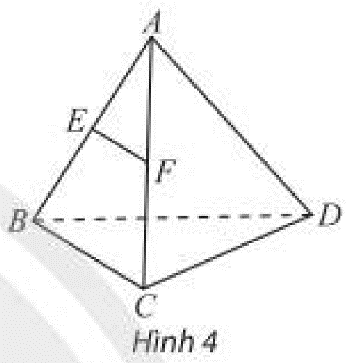
Gọi hệ trục Oxyz với A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0). Gọi S(p;q;h).
SA = SB = a:
p² + q² + h² = a²
(p - a)² + q² + h² = a² ⇒ p = a/2
SC = a√3:
a²/4 + (q - a)² + h² = 3a²
Từ SA: q² + h² = 3a²/4 ⇒ a²/4 + q² - 2aq + a² + h² = 3a²
2a² - 2aq = 3a² ⇒ q = -a/2 ⇒ h² = a²/2 ⇒ h = a√2/2
S(a/2; -a/2; a√2/2)
H(a/4; -a/4; a√2/4), K(3a/4; -a/4; a√2/4)
M(x; x; 0), 0 ≤ x ≤ a
N(a; t; 0) ∈ BC
HK = (a/2; 0; 0)
HM = (x - a/4; x + a/4; -a√2/4)
n = HK × HM = (0; a²√2/8; a/2(x + a/4))
Mặt phẳng (HKM): (a²√2/8)(y + a/4) + (a/2)(x + a/4)(z - a√2/4) = 0
Với N(a; t; 0): t = x ⇒ N(a; x; 0)
HK = a/2, MN = a - x
d = √[(x + a/4)² + a²/8]
S = (a/2 + a - x)/2 × d = (3a/2 - x)/2 × √[(x + a/4)² + a²/8]
Giải S'(x) = 0 ⇒ x = 5a/8
Kết luận: x = 5a/8 thì diện tích HKMN nhỏ nhất
Cho mình xin 1 tick với ạ








Ảnh của hình hộp ABEF.DCGH qua phép chiếu song song được mô tả trong hình 3 là hình hộp A'B'E'F'.D'C'G'H'