Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chọn A
đường thẳng đi qua \(2\) điểm \(A\left(-3;2\right)\) và \(B\left(1;4\right)\) có \(VTCP\) là :
\(\overrightarrow{AB}\) \(=\left(4;2\right)\) hoặc \(\overrightarrow{u}\) \(\left(2;1\right)\)

a: Vì (P) đi qua A(0;1); B(1;2); C(3;-1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0^2+b\cdot0+c=1\\a\cdot1^2+b\cdot1+c=2\\a\cdot3^2+b\cdot3+c=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=1\\a+b+1=2\\9a+3b+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=1\\a+b=1\\9a+3b=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=1\\9a+9b=9\\9a+3b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=1\\6b=11\\a+b=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=1\\b=\dfrac{11}{6}\\a=1-\dfrac{11}{6}=-\dfrac{5}{6}\end{matrix}\right.\)
b: Vì (P) đi qua M(0;-1); N(1;0) và P(2;3) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0^2+b\cdot0+c=-1\\a\cdot1^2+b\cdot1+c=0\\a\cdot2^2+b\cdot2+c=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=-1\\a+b-1=0\\4a+2b-1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-1\\a+b=1\\4a+2b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=-1\\a+b=1\\2a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-1\\-a=-1\\a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-1\\a=1\\b=0\end{matrix}\right.\)
c: Vì (P) đi qua M(1;-2); N(0;4); P(2;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot1^2+b\cdot1+c=-2\\a\cdot0^2+b\cdot0+c=4\\a\cdot2^2+b\cdot2+c=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a+b+c=-2\\c=4\\4a+2b+c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=4\\a+b=-2-c=-6\\4a+2b=1-4=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=4\\4a+4b=-24\\4a+2b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=4\\2b=-21\\a+b=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=4\\b=-\dfrac{21}{2}\\a=-6-b=-6+\dfrac{21}{2}=\dfrac{9}{2}\end{matrix}\right.\)
d: Hoành độ đỉnh là 2 nên -b/2a=2
=>b=-4a(1)
Thay x=3 và y=1 vào (P), ta được:
\(a\cdot3^2+b\cdot3+c=1\)
=>\(9a+3b+c=1\left(2\right)\)
Thay x=-1 và y=2 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+c=2\)
=>a-b+c=2(3)
Từ (1),(2),(3), ta có hệ phương trình:
\(\left\{{}\begin{matrix}b=-4a\\9a+3b+c=1\\a-b+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\9a-12a+c=1\\a+4a+c=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-4a\\-3a+c=1\\5a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\-8a=-1\\5a+c=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{1}{8}\\b=-4\cdot\dfrac{1}{8}=-\dfrac{1}{2}\\c=2-5a=2-\dfrac{5}{8}=\dfrac{11}{8}\end{matrix}\right.\)

a/ \(\overrightarrow{AB}=\left(1;1\right)\Rightarrow\) đường thẳng AB nhận \(\overrightarrow{n}=\left(1;-1\right)\) là 1 vtpt
Phương trình AB:
\(1\left(x-1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+1=0\)
b/ Gọi phương trình đường thẳng có dạng \(y=3x+b\)
Do đi qua \(A\left(1;4\right)\Rightarrow4=3.1+b\Rightarrow b=1\)
\(\Rightarrow y=3x+1\Leftrightarrow3x-y+1=0\)
c/ Phương trình đường thẳng:
\(1\left(x-3\right)+2\left(y-6\right)=0\Leftrightarrow x+2y-15=0\)
d/ Do \(\overrightarrow{u}=\left(2;3\right)\) là 1 vtcp nên đường thẳng nhận \(\overrightarrow{n}=\left(3;-2\right)\) là 1 vtpt
Phương trình:
\(3\left(x-1\right)-2\left(y+2\right)=0\Leftrightarrow3x-2y-7=0\)

a/ ĐK: \(3x+1\ge0\Rightarrow x\ge-\frac{1}{3}\)
\(x^2-7x+10=\left(3x+1\right)^2\)
\(\Leftrightarrow x^2-7x+10=9x^2+6x+1\)
\(\Leftrightarrow8x^2+13x-9=0\Rightarrow\left[{}\begin{matrix}x=\frac{-13-\sqrt{457}}{16}< -\frac{1}{3}\left(l\right)\\x=\frac{-13+\sqrt{457}}{16}\end{matrix}\right.\)
Pt có 1 nghiệm
b/ \(B\cap C=\varnothing\Rightarrow A\cap B\cap C=\varnothing\)
c/ Do \(VT\ge0\Rightarrow VP\ge0\Rightarrow-x\ge0\Rightarrow x\le0\)
Chỉ có đáp án A thỏa mãn, ko cần giải pt
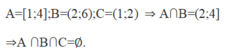
a: A hợp B hợp C
=[1;6) hợp (1;2)
=[1;6)
A giao B giao C
=(2;4] giao (1;2)
=\(\varnothing\)
b: A hợp B hợp C
=R hợp (0;4)
=R
A giao B giao C
=\(\varnothing\) giao (0;4)
=\(\varnothing\)