Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow-2}f\left(x\right)=\lim\limits_{x\rightarrow-2}\frac{x+2}{\left(x+2\right)\left(x-4\right)}=\lim\limits_{x\rightarrow-2}\frac{1}{x-4}=-\frac{1}{6}\)
\(f\left(-2\right)=-2a+1\)
Để hàm số liên tục (chứ ko phải có giới hạn) tại \(x=-2\) thì:
\(\lim\limits_{x\rightarrow-2}f\left(x\right)=f\left(-2\right)\Leftrightarrow-2a+1=-\frac{1}{6}\Rightarrow a=\frac{7}{12}\)
Bạn ghi sai đề, chắc chắn
Đầu tiên 2 biểu thức của \(f\left(x\right)\) ko liên quan đến nhau, nếu dòng đầu là \(x\ne2\) thì dòng 2 phải là \(x=2\), hoặc ngược lại
Tiếp theo, hàm số ko hề bị gián đoạn tại \(x=1\) (chẳng liên quan gì tới số 1 ở đây) nên chắc chắn hàm luôn có giới hạn tại \(x=1\) ko phụ thuộc vào tham số a

\(f\left(-1\right)=\lim\limits_{x\rightarrow-1^-}f\left(x\right)=\lim\limits_{x\rightarrow-1^-}\left(2-ax\right)=2+a\)
\(\lim\limits_{x\rightarrow-1^+}f\left(x\right)=\lim\limits_{x\rightarrow-1^+}\left(x^2-bx+2\right)=3+b\)
\(f\left(1\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(4x+a\right)=4+a\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(x^2-bx+2\right)=3-b\)
Hàm liên tục trên R khi và chỉ khi:
\(\left\{{}\begin{matrix}2+a=3+b\\4+a=3-b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-1\end{matrix}\right.\)

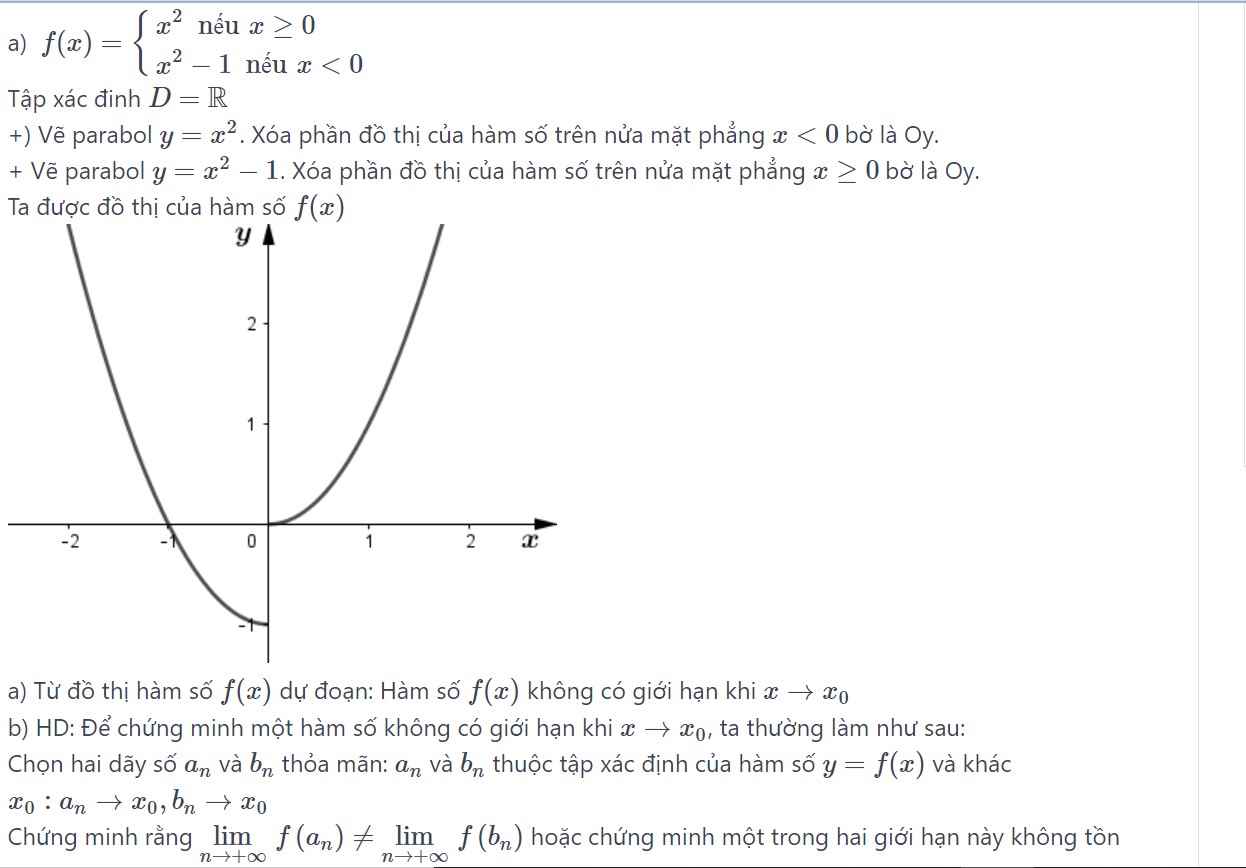
Hàm số liên tục tại mọi điểm khác 0 và 2
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+1\right)=1\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(x-1\right)^3=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow0^-}f\left(x\right)\ne\lim\limits_{x\rightarrow0^+}f\left(x\right)\)
\(\Rightarrow f\left(x\right)\) gián đoạn tại \(x_0=0\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(x-1\right)^3=1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(\sqrt{x}-1\right)=\sqrt{2}-1\)
\(\Rightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)\ne\lim\limits_{x\rightarrow2^+}f\left(x\right)\Rightarrow\) hàm số gián đoạn tại \(x_0=2\)

Tại mọi điểm \(x\ne1\) hàm đã cho là hàm đa thức nên liên tục
Xét tại \(x=1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(3x+2\right)=5\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(x^2-1\right)=0\)
Do \(\lim\limits_{x\rightarrow1^+}f\left(x\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\) nên hàm số đã cho ko liên tục tại \(x=1\)

\(\lim\limits_{x\rightarrow1^-}=f\left(1\right)=\lim\limits_{x\rightarrow1^-}\sqrt{4-x^2}=\sqrt{3}\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(x^2+bx+c\right)=b+c+1\)
Để hàm số liên tục tại x=1 \(\Rightarrow b+c+1=\sqrt{3}\)
\(f'\left(1^-\right)=\lim\limits_{x\rightarrow1^-}\frac{-x}{\sqrt{4-x^2}}=-\frac{1}{\sqrt{3}}\)
\(f'\left(1^+\right)=\lim\limits_{x\rightarrow1^+}\left(2x+b\right)=b+2\)
Để hàm số có đạo hàm tại \(x=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c+1=\sqrt{3}\\b+2=-\frac{1}{\sqrt{3}}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-2-\frac{1}{\sqrt{3}}\\c=1+\frac{4}{\sqrt{3}}\end{matrix}\right.\)
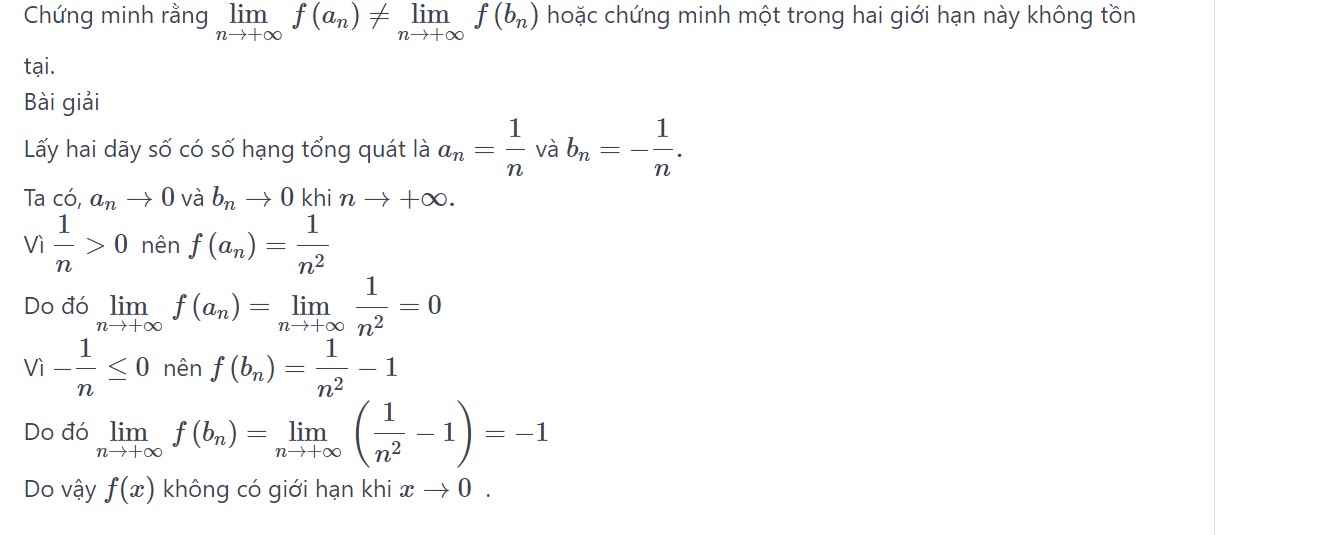
\(\lim\limits_{x\rightarrow-1^-}f\left(x\right)=2-a+b\)
\(\lim\limits_{x\rightarrow-1^+}f\left(x\right)=-4+2a\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=4+2a\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=a+b\)
Để hs có giới hạn tại \(x=1;-1\) thì:
\(\left\{{}\begin{matrix}2-a+b=-4+2a\\4+2a=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a-b=2\\a-b=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=7\end{matrix}\right.\)
4x+2a khi -1 <=x<1 nha mn