K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
24 tháng 6 2018
Giải:
\(a+b=10\)
\(\Leftrightarrow\left(a+b\right)^2=100\)
\(\Leftrightarrow a^2+2ab+b^2=100\)
\(\Leftrightarrow52+2ab=100\)
\(\Leftrightarrow2ab=48\)
\(\Leftrightarrow ab=24\)
Vậy ...
MC
24 tháng 6 2018
Theo bài ra: a + b = 10
⇒ a + b = 0 + 10 = 1 + 9 = 2 + 8 = 3 + 7 = 4 + 6 = 5 + 5
Thử từng trường hợp:
1) a + b = 0 + 10 ⇒ a2 + b2 = 02 + 102 = 100 ( loại )
2) a + b = 1 + 9 ⇒ a2 + b2 = 12 + 92 = 82 ( loại )
3) a + b = 2 + 8 ⇒ a2 + b2 = 22 + 82 = 68 ( loại )
4) a + b = 3 + 7 ⇒ a2 + b2 = 32 + 72 = 58 ( loại )
5) a + b = 4 + 6 ⇒ a2 + b2 = 42 + 62 = 52 ( thỏa mãn )
6) a + b = 5 + 5 ⇒ a2 + b2 = 52 + 52 = 50 ( loại )
⇒ a + b = 4 + 6
⇒ ab = 4 . 6 = 24
Vậy ab = 4 . 6 = 24
LT
0
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
\(\Leftrightarrow a^2-2a+1+b^2+6b+9=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-1=0\\b+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)
17 tháng 11 2019
a3 + b3=(a+b)(a2-ab+b2)
(a + b)3 =a3+b3+3ab(a+b)
a2 + b2=a2+2ab+b2
28 tháng 10 2021
\(\left(a+b\right)^2=\left(a-b\right)^2+4ab==2^2+4\cdot3=16\)
26 tháng 7 2023
1:
a: A=x^2+4x+4+13
=(x+2)^2+13>=13
Dấu = xảy ra khi x=-2
b; =x^2-8x+16+84
=(x-4)^2+84>=84
Dấu = xảy ra khi x=4
c: =x^2+x+1/4+19/4
=(x+1/2)^2+19/4>=19/4
Dấu = xảy ra khi x=-1/2
16 tháng 12 2018
a) \(a^2+b^2+1\ge ab+a+b\Leftrightarrow2a^2+2b^2+2\ge2ab+2a+2b\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra <=> a=b=1.
b) \(a^2-2a+6b+b^2=-10\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\). Mà \(\left(a-1\right)^2\ge0;\left(b+3\right)^2\ge0\forall a;b\)
Nên \(\hept{\begin{cases}\left(a-1\right)^2=0\\\left(b+3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=-3\end{cases}}}\). KL: ...
18 tháng 3 2020
Ta có: a+b+c=1 <=>(a+b+c)2 = 1 <=> ab+bc+ca=0 (1)
Theo dãy tỉ số bằng nhau ta có:
xa=yb=zc=x+y+za+b+c=x+y+z1=x+y+zxa=yb=zc=x+y+za+b+c=x+y+z1=x+y+z
<=> x = a(x+y+z) ; y = b(x+y+z) ; z = c(x+y+z)
=> xy+yz+zx= ab(x+y+z)2+bc(x+y+z)2+ca(x + y + z)2
<=> xy+yz+zx =(ab+bc+ca)(x+y+z)2 (2)
từ (1) và (2) => xy + yz + zx = 0
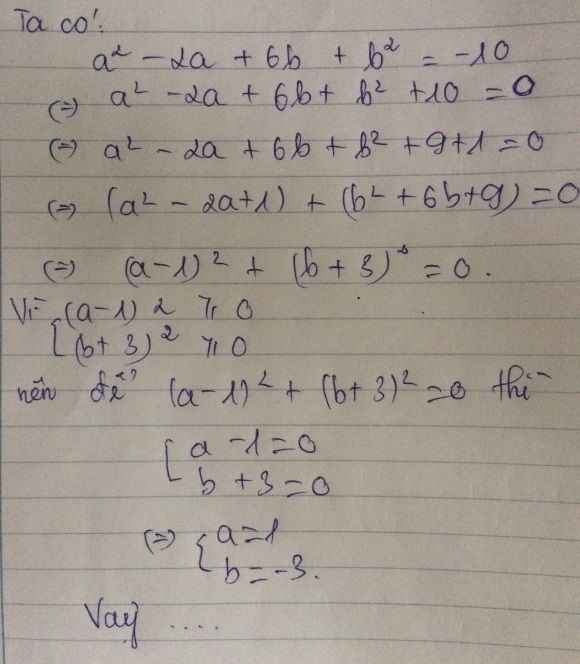
tìm m*n biết 5*m-2*n=30 ; 25*m^2+4*n^2=1200
1+1=3 Vì sao