Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để xác định các hệ số a và b ta dựa vào tọa độ các điểm mà đồ thị đi qua, lập hệ phương trình có hai ẩn a và b
a) Vì đồ thị đi qua \(A\left(\dfrac{2}{3};-2\right)\) nên ta có phương trình \(a.\dfrac{2}{3}+b=-2\)
Tương tự, dựa vào tọa độ của \(B\left(0;1\right)\) ta có \(0+b=1\)
Vậy, ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{2a}{b}+b=-2\\b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{9}{2}\\b=1\end{matrix}\right.\)
b) \(a=0;b=-2\)
c) \(a=\dfrac{1}{3};b=\dfrac{2}{3}\)

a) Thay x, y trong phương trình y = ax + b bằng tọa độ của A và của B ta được hệ phương trình:
Vậy phương trình của đường thẳng đi qua A(0; 3) và là: y = - 5x + 3.
b) Thay \(x,y\) trong phương trình \(y=ax+b\) bằng tọa độ A và B ta được hệ phương trình: \(\left\{{}\begin{matrix}1.a+b=2\\2.a+b=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\).
Vậy phương trình đường thẳng cần tìm là: \(y=-x+3\).
c) Thay \(x,y\) trong phương trình \(y=ax+b\) bằng tọa độ A và B ta được hệ phương trình: \(\left\{{}\begin{matrix}15a+b=-3\\21a+b=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-3\end{matrix}\right.\).
Vậy phương trình đường thẳng cần tìm là: \(y=-3\).

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4a=-28\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-13\end{matrix}\right.\)
b: Vì (d)//y=-2/3x+1 nên a=-2/3
Vậy: (d): y=-2/3x+b
Thay x=4 và y=-3 vào (d), ta được:
b-8/3=-3
hay b=-1/3

a)
y(1) =a-4+c=\(-2\)\(\Rightarrow\) a+c=2
y(2)=4a-8+c=3 \(\Rightarrow\)4a+c=3
Trừ cho nhau\(\Rightarrow\)3a=1 \(\Rightarrow\)a=\(\dfrac{1}{3}\)\(\Rightarrow\) \(c=2-\dfrac{1}{3}=\dfrac{5}{3}\).
Vậy: \(y=\dfrac{1}{3}x^2-4x+\dfrac{5}{3}\).
b)
I(-2;1)\(\Rightarrow\dfrac{4}{2a}=-2\)\(\Leftrightarrow a=-1\).
y(-2) \(=-4+8+c=1\)\(\Rightarrow\) \(c=-3\)
Vậy: \(y=-x^2-4x-3\).
c)\(\dfrac{4}{2a}=-3\)\(\Leftrightarrow a=-\dfrac{2}{3}\)
\(y\left(-2\right)=-\dfrac{2}{3}.4+8+c=1\)\(\Leftrightarrow c=-\dfrac{13}{3}\)
Vậy: \(y=-\dfrac{2}{3}x^3-4x-\dfrac{13}{3}\).

a) Phương trình đường thẳng (d) qua A(4; 3) và B(2;- 1) có dạng tổng quát là y = ax + b, trong đó a, b là các hằng số cần xác định.
Vì A(4; 3) ∈ d nên ta có phương trình của (d), do đó ta có: 3 = a.4 + b.
Tương tự B(2;- 1) ∈ d nên ta có: - 1 = a.2 + b
Từ đó ta tìm được phương trình đường thẳng AB là: y = 2x - 5.
Phương trình đường thẳng AB là: y = 2x - 5.
b) Đáp số: y = - 1.

Bài 1 : Đồ thị đi qua điểm M(4;-3) \(\Rightarrow\) y=-3 x=4. Ta được:
\(-3=4a+b\)
Đồ thị song song với đường d \(\Rightarrow\) \(a=a'=-\dfrac{2}{3}\) Ta được:
\(-3=4.-\dfrac{2}{3}+b\) \(\Rightarrow\) \(b=-\dfrac{1}{3}\)
Vậy: \(a=-\dfrac{2}{3};b=-\dfrac{1}{3}\)
b) (P) đi qua 3 điểm A B O, thay tất cả vào (P), ta được hpt:
\(\hept{\begin{cases}a+b+c=1\\a-b-c=-3\\0+0+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=-1\\b=2\\c=0\end{cases}}}\)
Bài 2 : Mình ko biết vẽ trên này, bạn theo hướng dẫn rồi tự làm nhé
Đồ thị có \(a< 0\) \(\Rightarrow\) Hàm số nghịch biến trên R
\(\Rightarrow\) Đồ thị có đỉnh \(I\left(1;4\right)\)
Chọn các điểm:
x 1 3 -1 2 -2
y 4 0 0 3 -5

a) f(x) = (x+2)(x-1)
f(x) > 0 với x < -2 hoặc x > 1
f(x) ≤ 0 với -2 ≤ x ≤ 1
b) y = 2x (x + 2) = 2(x+1)2 – 2
Bảng biến thiên:
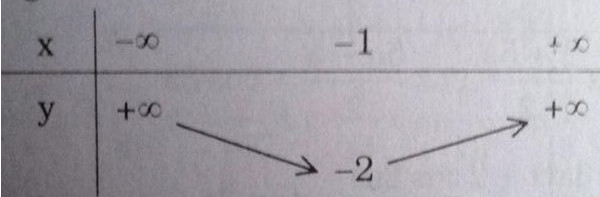
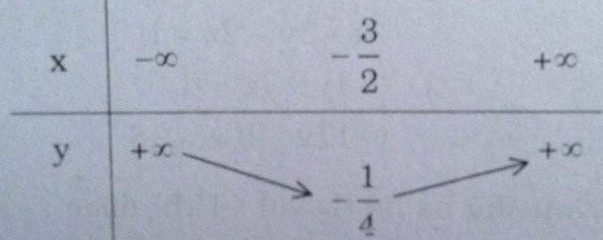
Hàm số : y = \(\left(x+2\right)\left(x+1\right)=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\)
Bảng biến thiên :
Đồ thị (C1) và (C2)
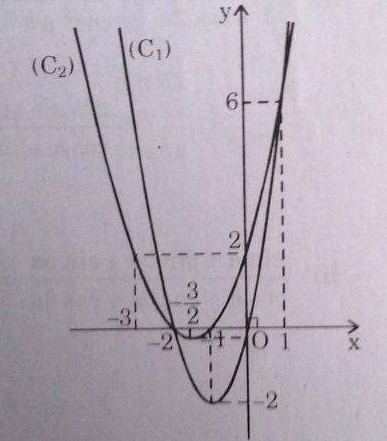
Hoành độ các giao điểm A và B của (C1) và (C2) là nghiệm của phương trình f(x) = 0 ⇔ x1 = -2, x2 = 1
⇔ A(-2, 0) , B(1, 6)
c) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{ac-b^2}{4a}\\a\left(-2\right)^2+b\left(-2\right)+c=0\\a\left(1\right)^2+b\left(1\right)+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2,b=0,c=8\\a=-\dfrac{2}{9},b=\dfrac{16}{9},c=\dfrac{40}{9}\end{matrix}\right.\)

mình nghĩ pt (P) : y = ax^2 - bx + c chứ ?
a, (P) đi qua điểm A(0;-1) <=> \(c=-1\)
(P) đi qua điểm B(1;-1) <=> \(a-b+c=-1\)(1)
(P) đi qua điểm C(-1;1) <=> \(a+b+c=1\)(2)
Thay c = -1 vào (1) ; (2) ta được : \(a-b=0;a+b=2\Rightarrow a=1;b=1\)
Vậy pt Parabol có dạng \(x^2-x-1=y\)
Bài 1b
(P) đi qua điểm A(8;0) <=> \(64a-8b+c=0\)
(P) có đỉnh I(6;12) \(\Rightarrow\hept{\begin{cases}-\frac{b}{2a}=6\\36a-6b+c=-12\end{cases}}\Rightarrow a=3;b=-36;c=96\)
Vậy pt Parabol có dạng : \(9x^2+36x+96=y\)
tương tự nhé

a) Bảng biến thiên

Đồ thị hàm số
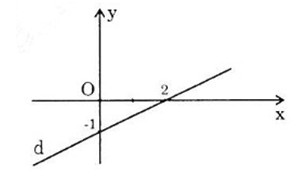
Đồ thị là đường thẳng đi qua 2 điểm:
+ Giao với trục tung P(0,-1)
+ Giao với trục hoành Q(2, 0)
b) Bảng biến thiên

Đồ thị hàm số
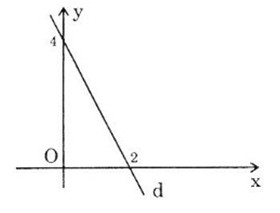
Đồ thị là đường thẳng đi qua 2 điểm:
+ Giao với trục tung P(0,4)
+ Giao với trục hoành Q(2, 0)
c) y=√x2y=x2 = |x| ={−x,x≤0x,x>0{−x,x≤0x,x>0
Bảng biến thiên
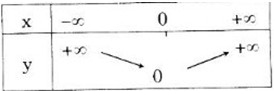
Đồ thị hàm số
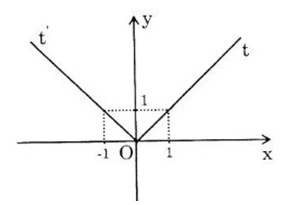
d) y = |x+1| = {−x−1,x≤−1x+1,x>−1{−x−1,x≤−1x+1,x>−1
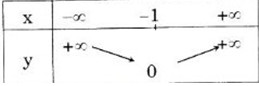
Bảng biến thiên
Đồ thị hàm số
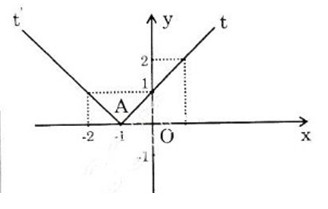
Đồ thị hàm số đi qua các điểm A, B nên ta có:
Chọn D.