Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ĐKXĐ \(a\ge0,a\ne\dfrac{1}{4},a\ne1\)
\(\Rightarrow P=1+\left(\dfrac{\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}-\dfrac{\sqrt{a}\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{2\sqrt{a}-1}\)
= \(1+\left(\dfrac{\left(-1\right)\left(2\sqrt{a}-1\right)}{\sqrt{a}-1}+\dfrac{\sqrt{a}\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{2\sqrt{a}-1}\)
= \(1+\left(-1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{a+\sqrt{a}+1}\right)\sqrt{a}\)
= \(1-\sqrt{a}+\dfrac{a\sqrt{a}+a}{a+\sqrt{a}+1}\) = \(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)+a\sqrt{a}+a}{a+\sqrt{a}+1}=\dfrac{1-a\sqrt{a}+a\sqrt{a}+a}{a+\sqrt{a}+1}=\dfrac{a+1}{a+\sqrt{a}+1}\)
b Xét hiệu \(P-\dfrac{2}{3}=\dfrac{a+1}{a+\sqrt{a}+1}-\dfrac{2}{3}=\dfrac{3a+3-2a-2\sqrt{a}-2}{a+\sqrt{a}+1}=\dfrac{a-2\sqrt{a}+1}{a+\sqrt{a}+1}=\dfrac{\left(\sqrt{a}-1\right)^2}{a+\sqrt{a}+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}>0\) \(\Rightarrow P>\dfrac{2}{3}\)
c Ta có \(P=\dfrac{\sqrt{6}}{\sqrt{6}+1}\Rightarrow\dfrac{a+1}{a+\sqrt{a}+1}=\dfrac{\sqrt{6}}{\sqrt{6}+1}\) \(\Rightarrow\left(a+1\right)\left(\sqrt{6}+1\right)=\sqrt{6}\left(a+\sqrt{a}+1\right)\Leftrightarrow a\sqrt{6}+a+\sqrt{6}+1=a\sqrt{6}+\sqrt{6a}+\sqrt{6}\)
\(\Leftrightarrow a-\sqrt{6a}+1=0\Leftrightarrow a-\sqrt{6a}+\dfrac{6}{4}-\dfrac{2}{4}=0\Leftrightarrow\left(\sqrt{a}-\dfrac{\sqrt{6}}{2}\right)^2=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{a}=\dfrac{\sqrt{6}+1}{2}\\\sqrt{a}=\dfrac{1-\sqrt{6}}{2}\left(L\right)\end{matrix}\right.\) (Do \(\sqrt{a}\ge0\)) \(\Rightarrow a=\dfrac{\left(\sqrt{6}+1\right)^2}{4}=\dfrac{7+2\sqrt{6}}{4}\left(TM\right)\)
Vậy...

ĐKXĐ: \(a>0;a\ne1\)
\(\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{a-\sqrt{a}}\right):\dfrac{\sqrt{a}+1}{a-1}\)
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right).\dfrac{a-1}{\sqrt{a}+1}\)
\(=\left[\dfrac{\sqrt{a}.\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right].\dfrac{a-1}{\sqrt{a}+1}\)
\(=\left[\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\right].\dfrac{a-1}{\sqrt{a}+1}\)
\(=\dfrac{\sqrt{a}-2}{\sqrt{a}-1}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-2\)

Sửa đề: \(C=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(a,C=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\left(a>0;a\ne1;a\ne4\right)\\ C=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\\ b,C\ge\dfrac{1}{6}\Leftrightarrow\dfrac{\sqrt{a}-2}{3\sqrt{a}}-\dfrac{1}{6}\ge0\Leftrightarrow\dfrac{\sqrt{a}-4}{6\sqrt{a}}\ge0\\ \Leftrightarrow\sqrt{a}-4\ge0\left(6\sqrt{a}>0\right)\\ \Leftrightarrow a\ge16\)

1)Để căn có nghĩa \(\Leftrightarrow\dfrac{-a}{3}\ge0\Leftrightarrow a\le0\)
Vậy...
2)Để căn có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a^2+1}{1-3a}\ge0\\1-3a\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}1-3a>0\left(vìa^2+1>0\right)\\1-3a\ne0\end{matrix}\right.\)
\(\Leftrightarrow1-3a>0\Leftrightarrow3a< 1\Leftrightarrow a< \dfrac{1}{3}\)
Vậy...
3)Để căn có nghĩa
\(\Leftrightarrow a^2-6a+10\ge0\Leftrightarrow\left(a^2-6a+9\right)+1\ge0\Leftrightarrow\left(a-3\right)^2+1\ge0\left(lđ;\forall a\right)\)
Vậy căn luôn có nghĩa với mọi a
4)Để căn có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a-1}{a+2}\ge0\\a+2\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}\left\{{}\begin{matrix}a-1\ge0\\a+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}a-1\le0\\a+2< 0\end{matrix}\right.\end{matrix}\right.\\a+2\ne0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a\ge1\\a>-2\end{matrix}\right.\\\left\{{}\begin{matrix}a\le1\\a< -2\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}a\ge1\\a< -2\end{matrix}\right.\)
Vậy...

\(a,M=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\\ M=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\\ b,M< \dfrac{1}{6}\Leftrightarrow\dfrac{\sqrt{a}-2}{3\sqrt{a}}-\dfrac{1}{6}< 0\\ \Leftrightarrow\dfrac{2\sqrt{a}-4-\sqrt{a}}{6\sqrt{a}}< 0\Leftrightarrow\dfrac{\sqrt{a}-4}{6\sqrt{a}}< 0\\ \Leftrightarrow\sqrt{a}-4< 0\left(6\sqrt{a}>0\right)\\ \Leftrightarrow a< 16\\ \Leftrightarrow0< a< 16\left(kết.hợp.ĐKXĐ\right)\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
c: Ta có: \(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
\(\Leftrightarrow\dfrac{2}{x+\sqrt{x}+1}>0\forall x\)

b)CM: \(ab\sqrt{1+\dfrac{1}{a^2b^2}}-\sqrt{a^2b^2+1}=0\)
\(VT=ab\sqrt{\dfrac{a^2b^2+1}{\left(ab\right)^2}}-\sqrt{a^2b^2+1}\)
\(VT=ab\dfrac{\sqrt{a^2b^2+1}}{ab}-\sqrt{a^2b^2+1}\)
\(VT=\sqrt{a^2b^2+1}-\sqrt{a^2b^2+1}\)
\(VT=0=VP\)



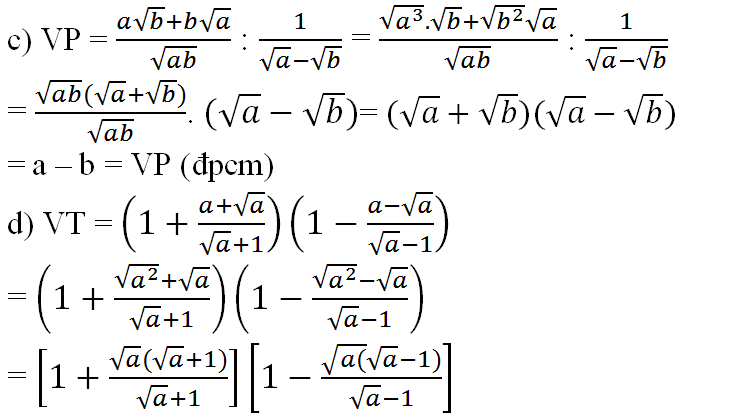
\(\dfrac{1+a}{1+\sqrt{a}+1}=\dfrac{\sqrt{6}}{1+\sqrt{6}}\\ \Leftrightarrow\left(1+\sqrt{6}\right)\left(1+a\right)=\sqrt{6}\left(1+\sqrt{a}+a\right)\\ \Leftrightarrow1+a+\sqrt{6}+\sqrt{6}a=\sqrt{6}+\sqrt{6}a+\sqrt{6}a\\ \Leftrightarrow1+a=\sqrt{6}a\\ \Leftrightarrow\sqrt{6}a=1+a\\ \Leftrightarrow6a=1+2a+a^2\\ \Leftrightarrow6a-1-2a-a^2=0\\ \Leftrightarrow4a-1-a^2=0\\ \Leftrightarrow-a^2+4a-1=0\\ \Leftrightarrow a^2-4a+1=0\)
\(a=\dfrac{-\left(-4\right)\pm\sqrt{\left(-4\right)^2-4.1.1}}{2.1}\\ a=\dfrac{4\pm\sqrt{16-4}}{2}\\ a=\dfrac{4\pm\sqrt{12}}{2}\\ a=\dfrac{4\pm2\sqrt{3}}{2}\)
\(\left[{}\begin{matrix}a=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\\a=\dfrac{4-2\sqrt{3}}{2}=2-\sqrt{3}\end{matrix}\right.\)
Vậy......
Sr bạn cách làm mình hơi khó hiểu chút :v
a)ĐK: \(a\ge0\)
\(\Leftrightarrow\left(1+a\right)\left(1+\sqrt{6}\right)=\sqrt{6}\left(a+\sqrt{a}+1\right)\)
\(\Leftrightarrow1+\sqrt{6}+a+a\sqrt{6}=a\sqrt{6}+\sqrt{6a}+\sqrt{6}\)
\(\Leftrightarrow1+a=\sqrt{6a}\)
\(\Leftrightarrow a^2+2a+1-6a=0\)
\(\Leftrightarrow a^2-4a+1=0\)
\(\Leftrightarrow\left(a-2\right)^2-3=0\)
\(\Leftrightarrow\left(a-2\right)^2=3\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-2=\sqrt{3}\\a-2=-\sqrt{3}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\sqrt{3}+2\\a=2-\sqrt{3}\end{matrix}\right.\)
b)
MK sẽ chứng minh tương đương:
\(\Leftrightarrow\dfrac{1+a}{1+\sqrt{a}+a}-\dfrac{2}{3}>0\)
\(\Leftrightarrow\dfrac{a-2\sqrt{a}+1}{1+\sqrt{a}+a}>0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{a}-1\right)^2}{1+\sqrt{a}+a}>0\)
Ta có:
\(\left(\sqrt{a}-1\right)^2\ge0\left(1\right)\)
\(1+\sqrt{a}+a=\left(\sqrt{a}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà \(\left(\sqrt{a}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\Leftrightarrow1+\sqrt{a}+a>0\left(2\right)\)
Từ (1), (2)
=>\(\dfrac{\left(\sqrt{a}-1\right)^2}{1+\sqrt{a}+a}>0\)
=>\(\dfrac{1+a}{1+\sqrt{a}+a}>\dfrac{2}{3}\)