Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=-1\\2a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)

Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=-1\\4a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\)

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

b: \(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-4=2m-1\\x^2-3x-4=-2m+1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-3x-4-2m+1=0\\x^2-3x-4+2m-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-2m+3=0\\x^2-3x+2m-5=0\end{matrix}\right.\)
Để phương trình có bốn nghiệm phân biệt thì \(\left\{{}\begin{matrix}9-4\left(-2m+3\right)>0\\9-4\left(2m-5\right)>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9+8m-12>0\\9-8m+20>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8m>3\\8m< 29\end{matrix}\right.\Leftrightarrow\dfrac{3}{8}< m< \dfrac{29}{8}\)

a) Tập xác định D = R
Bảng biến thiên
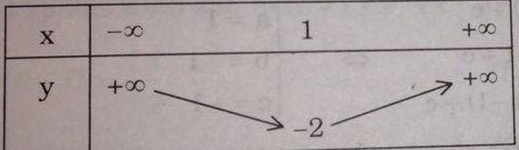
Đồ thị hàm số
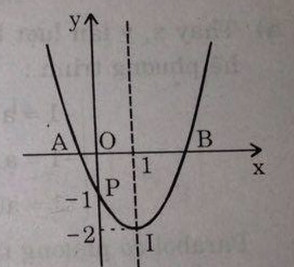
Đồ thị: parabol có đỉnh I(1, -2) với trục đối xứng x = 1
Giao điểm với trục tung là P(0,-1)
Giao điểm với trục hoành A (1-√2, 0) và B((1+√2, 0)
b)
Tập xác định D = R
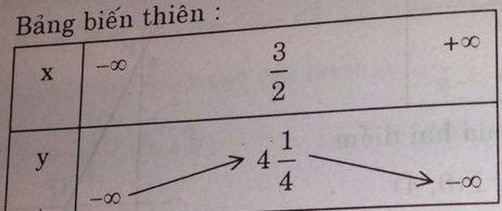
Đồ thị hàm số
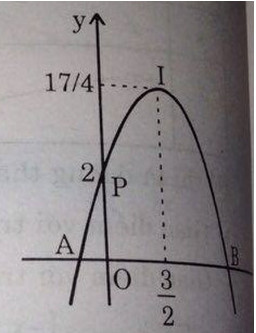
Đồ thị: parabol có đỉnh I \(\left(\dfrac{3}{2},\dfrac{17}{4}\right)\)với trục đối xứng \(x=\dfrac{3}{2}\)
Giao điểm với trục tung là P(0,2)
Giao điểm với trục hoành A \(\left(\dfrac{3-\sqrt{17}}{2},0\right)\) và B\(\left(\dfrac{3+\sqrt{17}}{2},0\right)\)

a, Bảng biến thiên:
Đồ thị hàm số:
b, Phương trình hoành độ giao điểm
\(-x^2+2x+3=4x-5\)
\(\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
Nếu \(x=2\Rightarrow y=3\Rightarrow\left(2;3\right)\)
Nếu \(x=-4\Rightarrow y=-21\Rightarrow\left(-4;-21\right)\)
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b+1=0\\2a+b+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-1\\2a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)
bạn giải kỹ hơn đc ko