K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
21 tháng 1 2018
a) √911 = √9,11.√100 = 3,018.10 = 30,18
b) √988 = √9,88.√100 = 3,143.10 = 31,43
TM
1
12 tháng 8 2023
a:
ĐKXĐ: x>0; x<>1\(M=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\left(\sqrt{x}+1\right)^2-4\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x+2\sqrt{x}+1-4\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}}{x-2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
b: M là số nguyên
=>\(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>căn x-2 thuộc {1;-1}
=>căn x thuộc {3;1}
=>x thuộc {9;1}
Kết hợp ĐKXĐ, ta được: x=9
c: M<0
=>\(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}< 0\)
=>\(1< \sqrt{x}< 2\)
=>1<x<4
23 tháng 9 2021
+)Muốn tính \(\cot\) bằng máy tính, bạn ấn \(\dfrac{1}{\tan\left(...\right)}\) (...) là số đo góc
Từ số ra góc thì bạn ấn Shift + nút \(\sin,\cos,\tan\) rồi nhập tỉ số lượng giác vô thì ra số đo góc nha
+)\(\sin^2x=\sin x\cdot\sin x;\sin x^2=\sin\left(x\cdot x\right)\)
\(\Rightarrow\sin^2x\ne\sin x^2\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
ĐKXĐ: \(x\ge0;x\ne4\)
\(A=\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b. \(x=36\Rightarrow A=\dfrac{\sqrt{36}}{\sqrt{36}-2}=\dfrac{6}{6-2}=\dfrac{3}{2}\)
c. \(A=-\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{\sqrt{x}-2}=-\dfrac{1}{3}\Rightarrow3\sqrt{x}=2-\sqrt{x}\)
\(\Rightarrow4\sqrt{x}=2\Rightarrow\sqrt{x}=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{4}\)
d. \(A>0\Rightarrow\dfrac{\sqrt{x}}{\sqrt{x}-2}>0\Rightarrow\sqrt{x}-2>0\Rightarrow x>4\)
e. \(A=\dfrac{\sqrt{x}-2+2}{\sqrt{x}-2}=1+\dfrac{2}{\sqrt{x}-2}\in Z\Rightarrow\sqrt{x}-2=Ư\left(2\right)\)
\(\Rightarrow\sqrt{x}-2=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow\sqrt{x}=\left\{0;1;3;4\right\}\Rightarrow x=\left\{0;1;9;16\right\}\)
12 tháng 8 2021
a: Ta có: \(A=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b: Thay x=36 vào A, ta được:
\(A=\dfrac{6}{6-2}=\dfrac{6}{4}=\dfrac{3}{2}\)
c: Để \(A=-\dfrac{1}{3}\) thì \(3\sqrt{x}=-\sqrt{x}+2\)
\(\Leftrightarrow4\sqrt{x}=2\)
hay \(x=\dfrac{1}{4}\)
27 tháng 8 2021
a: Để hàm số đồng biến thì 2m-3>0
hay \(m>\dfrac{3}{2}\)
Để hàm số nghịch biến thì 2m-3<0
hay \(m< \dfrac{3}{2}\)
b: Thay x=2 và y=5 vào hàm số, ta được:
\(\left(2m-3\right)\cdot2+4=5\)
\(\Leftrightarrow2m-3=\dfrac{1}{2}\)
\(\Leftrightarrow2m=\dfrac{7}{2}\)
hay \(m=\dfrac{7}{4}\)
15 tháng 4 2021
b, Để phương trình có 2 nghiệm \(\Delta\ge0\)
hay \(\left(2m+8\right)^2-4.m^2=4m^2+32m+64-4m^2=32m+64\ge0\)
\(\Leftrightarrow32m\ge64\Leftrightarrow m\ge2\)
Theo Vi et ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+8\\x_1x_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
mà \(\left(x_1+x_2\right)^2=4m^2+32m+64\Rightarrow x_1^2+x_2^2=4m^2+32m+64-2x_1x_2\)
\(=4m^2+32m+64-2m^2=2m^2+32m+64\)
Lại có : \(x_1^2+x_2^2=-2\)hay \(2m^2+32m+66=0\Leftrightarrow m=-8+\sqrt{31}\left(ktm\right);m=-8-\sqrt{31}\left(ktm\right)\)
15 tháng 4 2021
a) Thay m=8 vào phương trình, ta được:
\(x^2-2\cdot\left(8+4\right)x+8^2=0\)
\(\Leftrightarrow x^2-24x+64=0\)
\(\text{Δ}=\left(-24\right)^2-4\cdot1\cdot64=576-256=320\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{24+8\sqrt{5}}{2}=12+4\sqrt{5}\\x_2=\dfrac{24-8\sqrt{5}}{2}=12-4\sqrt{5}\end{matrix}\right.\)
Vậy: Khi m=8 thì phương trình có hai nghiệm phân biệt là \(x_1=12+4\sqrt{5};x_2=12-4\sqrt{5}\)
EN
2
17 tháng 8 2021
a: Ta có: \(N=\dfrac{4\sqrt{x}-7}{x+\sqrt{x}-2}+\dfrac{2-\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{4\sqrt{x}-7+4-x-2x+\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-3x+5\sqrt{x}-4}{x+\sqrt{x}-2}\)
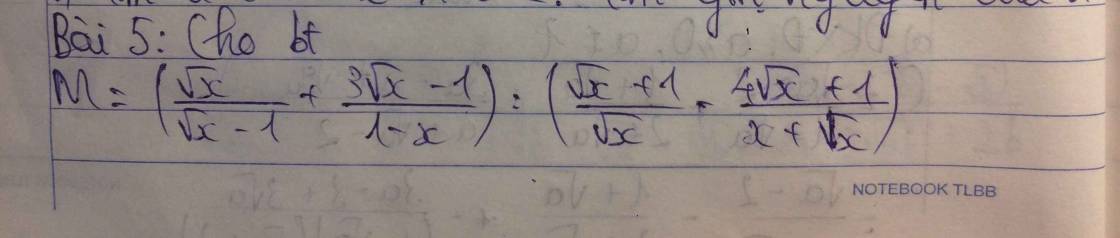
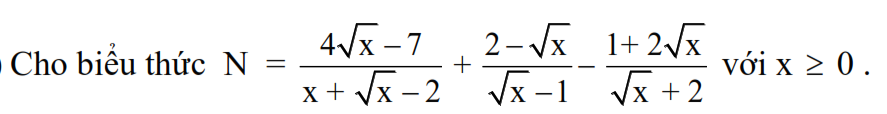
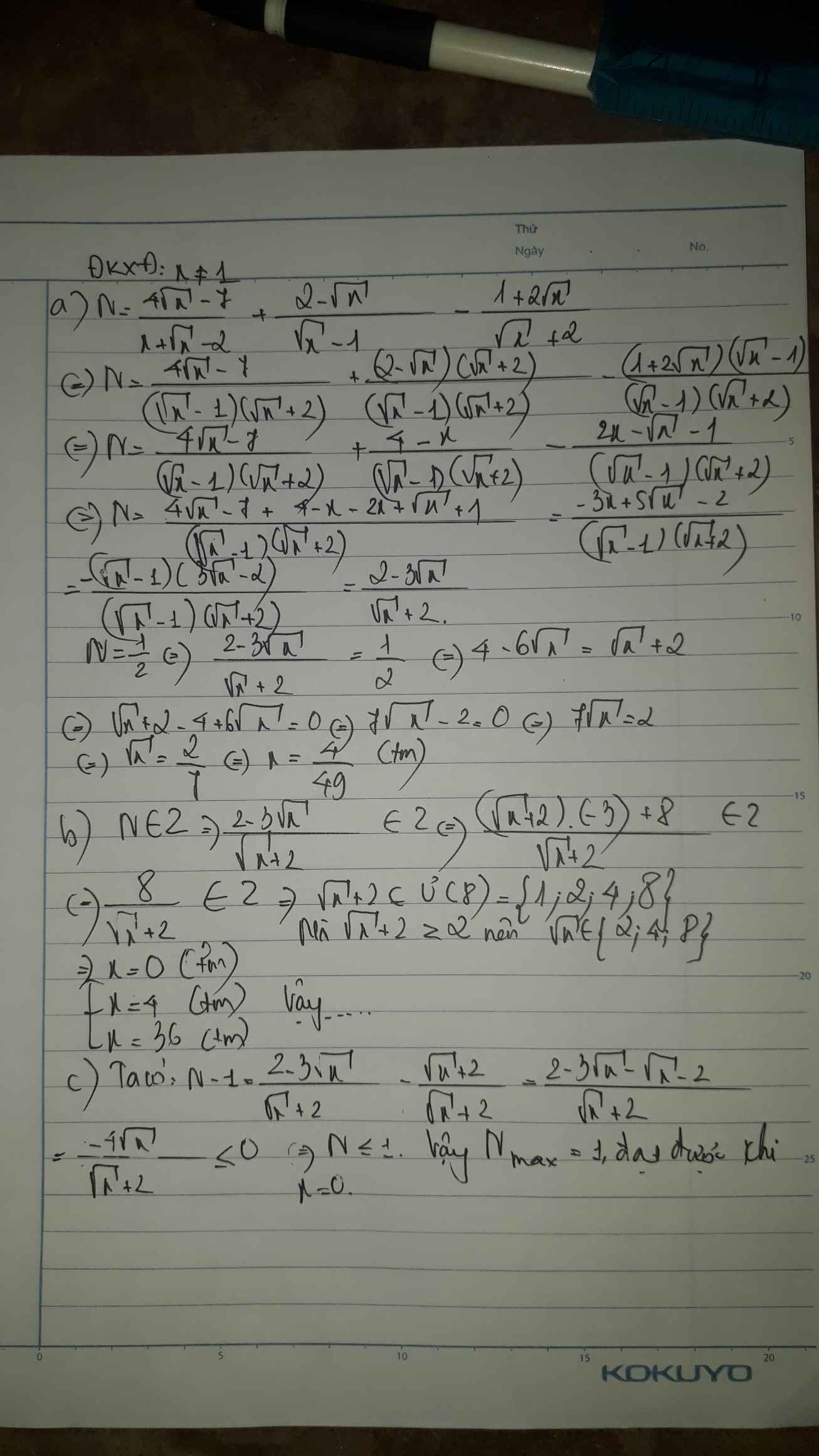
√988 = √9,88.√100 = 3,143.10 = 31,43