Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18

Chọn D
- Gọi u 1 , u 2 , . . . , u 7 là cấp số nhân cần tìm và q là công bội của cấp số nhân đó.
- Giả thiết ta có:
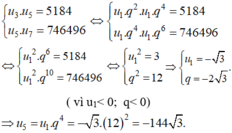

Kí hiệu u1,u2,u3,u4,u5 là các số hạng của cấp số nhân
Ta có :
![]()
![]()
![]()
![]()
![]()
![]()
Đáp án C

Gọi 3 số đó là: \(a,b,c\). Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b+c=114\\b^2=ac\end{matrix}\right.\). (*)
Mặt khác nó lần lượt là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng nên: \(a=u_1;b=u_1+3d;c=u_1+24d\). ( với \(u_1\) là số hạng đầu của cấp số cộng, d là công sai).
Thay vào (*) ta có:
\(\left\{{}\begin{matrix}u_1+u_1+3d+u_1+24d=114\\\left(u_1+3d\right)^2=u_1\left(u_1+24d\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\18u_1d-9d^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\9d\left(2u_1-d\right)=0\end{matrix}\right.\).
Nếu \(d=0\) thì a,b,c là ba số hạng của một cấp số cộng không đổi nên \(a=b=c=\sqrt[3]{114}\).
Nếu \(d\ne0\) suy ra: \(\left\{{}\begin{matrix}u_1+9d=38\\2u_1-d=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=2\\d=4\end{matrix}\right.\).
Khi đó \(a=2;b=2+3.4=16;c=2+24.3=74\).

Gọi cấp số nhân tăng nghiêm ngặt là \(a_n\). Theo đầu bài ta có \(a_2,a_4\) là 2 nghiệm của phương trình
\(t^2-30t+144=0\Leftrightarrow\begin{cases}t=6\\t=24\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2=6\\a_4=24\end{cases}\) hoặc \(\begin{cases}a_2=24\\a_4=6\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1q=6\\a_1q^3=24\end{cases}\) hoặc \(\begin{cases}a_1q=24\\a_1q^3=6\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1q=6\\q^2=4\end{cases}\) hoặc \(\begin{cases}a_1q=24\\q^2=\frac{6}{24}=\frac{1}{4}\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1=\frac{6}{\pm2}\\q=\pm2\end{cases}\) hoặc \(\begin{cases}a_1=24\left(\pm2\right)\\q=\pm\frac{1}{2}\end{cases}\)
Do cấp số nhân tăng nghiêm ngặt, nên q>1, do vậy ta chọn \(a_1=3;q=2\)
Cho nên \(S_{10}=u_1\frac{2^{10}-1}{2-1}=3.\left(1024-1\right)=3069\)
Giao lưu:
Gọi dãy số đã co có dạng: \(U_1;U_2;U_3;U_4;U_5...U_{10}...U_n\)
đầu bài ta có hệ phương trình.
\(\left\{\begin{matrix}U_n.q=U_{\left(n+1\right)}\left(1\right)\\q>1\left(2\right)\\U_2+U_4=144\left(3\right)\\U_2.U_4=30\left(4\right)\end{matrix}\right.\)
Thế (3) vào (4) \(\Leftrightarrow U_2\left(144-U_2\right)=30\Leftrightarrow U_2^2-144U_4+30=0\Rightarrow\left[\begin{matrix}U_2=24\\U_2=6\end{matrix}\right.\)
Vì U2 và U4 có vai trò như nhau
do vậy có cắp nghiệm là hoán đổi (U2,U4)=(6,24)(*)
Từ (1) và (2) ta có(*)=> \(\left\{\begin{matrix}U_2=6\\U_4=24\end{matrix}\right.\)(**)
Từ (1) ta có: \(U_4=q.U_3=q.\left(q.U_2\right)=q^2.U_2\)(4)
Từ (**) và (4) ta có \(\frac{U_4}{U_2}=q^2=\frac{24}{6}=4\Rightarrow!q!=2\) (5)
Từ (3) và (5) => q=2
Vậy tổng 10 số hạng đầu tiên của dẫy là :\(S_{10}=2^0.3+2^1.3+3.2^2+...+3.2^8+3.2^9=3.\left(1+2+2^2+..+2^9\right)\)
\(S_{10}=3.\left(2^{10}-1\right)\)

Gọi ba số đã cho u1,u2,u7 theo thứ tự là ba số của một cấp số cộng (un) và v1,v2, v3 của cấp số nhân (vn) . Theo giả thiết Ta có hệ:
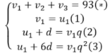
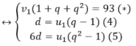
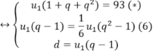
Giải phương trình (6)
( 6 ) ⇔ u 1 q − 1 = 1 6 u 1 q − 1 q + 1 ⇔ u 1 q − 1 = 0 ( l o a i ) 1 = 1 6 q + 1
Thay vào (*), ta được
u 1 1 + 5 + 5 2 = 93 ⇔ u 1 = 3 = v 1
Suy ra
u 2 = u 1 . q = 3.5 = 15 = v 2 u 3 = u 1 . q 2 = 3.25 = 75 = v 3
Vậy tích ba số v 1 . v 2 . v 3 = 3.15.75 = 3375
Đáp án A
Lời giải:
Gọi công bội là $q$ thì 3 số hạng trên là $a; aq; aq^2$
Theo bài ra ta có:
$a+aq+aq^2=a(1+q+q^2)=\frac{a(q^3-1)}{q-1}=19(*)$
$a.aq.aq^2=(aq)^3=216=6^3$
$\Rightarrow aq=6\Rightarrow a=\frac{6}{q}$. Thay vào $(*)$ và giải pt ẩn $q$ thôi bạn.