Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Các phát biểu đúng là 2, 3, 5, 6.
+ Mệnh đề 1: các axit béo no thường có nhiệt độ nóng chảy cao hơn axit béo không no.
+ Mệnh đề 4: Fructozo tồn tại chủ yếu ở dạng β, vòng 5 cạnh hoặc 6 cạnh

Đáp án A
Các phát biểu đúng là 2, 3, 5, 6.
+ Mệnh đề 1: các axit béo no thường có nhiệt độ nóng chảy cao hơn axit béo không no.
+ Mệnh đề 4: Fructozo tồn tại chủ yếu ở dạng β, vòng 5 cạnh hoặc 6 cạnh

Đáp án A
(a) Điện phân NaCl nóng chảy.
(b) Điện phân dung dịch CuSO4 (điện cực trơ).
(c) Cho mẩu K vào dung dịch AlCl3.
(g) Cho Cu vào dung dịch hỗn hợp Cu(NO3)2 và NaHSO4.

Chọn đáp án A.
a) 2 N a C l → 2 N a + C l 2
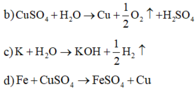
e) Không xảy ra phản ứng
![]()
=> Có 4 thí nghiệm sinh chất khí

phương trình dạng toán tử : \(\widehat{H}\)\(\Psi\) = E\(\Psi\)
Toán tử Laplace: \(\bigtriangledown\)2 = \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\)
thay vào từng bài cụ thể ta có :
a.sin(x+y+z)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))sin(x+y+z)
=\(\frac{\partial^2}{\partial x^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial y^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial z^2}\)sin(x+y+z)
=\(\frac{\partial}{\partial x}\)cos(x+y+z) + \(\frac{\partial}{\partial y}\)cos(x+y+z) + \(\frac{\partial}{\partial z}\)cos(x+y+z)
= -3.sin(x+y+z)
\(\Rightarrow\) sin(x+y+z) là hàm riêng. với trị riêng bằng -3.
b.cos(xy+yz+zx)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))cos(xy+yz+zx)
=\(\frac{\partial^2}{\partial x^2}\)cos(xy+yz+zx) +\(\frac{\partial^2}{\partial y^2}\)cos(xy+yz+zx) + \(\frac{\partial^2}{\partial z^2}\)cos(xy+yz+zx)
=\(\frac{\partial}{\partial x}\)(y+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial y}\)(x+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial z}\)(y+x).-sin(xy+yz+zx)
=- ((y+z)2cos(xy+yz+zx) + (x+z)2cos(xy+yz+zx) + (y+x)2cos(xy+yz+zx))
=-((y+z)2+ (x+z)2 + (x+z)2).cos(xy+yz+zx)
\(\Rightarrow\) cos(xy+yz+zx) không là hàm riêng của toán tử laplace.
c.exp(x2+y2+z2)

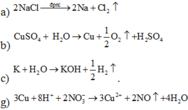
Đáp án A
X + NaOH + HCl → hh muối ( có muối NaCl) + 2 ancol đơn chức
→ X là este 2 chức tạo bởi axit 2 chức và 2 ancol đơn chức.
Có n(NaOH đầu) = 0,2 mol; n(NaOH dư) = n(HCl) = 0,04 mol.
→ n(NaOH phản ứng) = 0,2 – 0,04 = 0,16 mol.
(RCOO)2R’R’’ + 2NaOH → 2R(COONa)2 + R’OH + R’’OH
0,08 ← 0,16 → 0,08 0,08 0,08
NaOH + HCl → NaCl + H2O
=> m(muối) = m(NaCl) + m(RCOONa) = 0,04.58,5 + 0,08.(R+67.2) = 15,14 → R = 26 → C2H2.
→ T có công thức: HOOC-CH=CH-COOH (C4H4O4).
BTKL: mX = m(muối T) + m(ancol) – m(NaOH phản ứng) = 12,8 + 7,36 – 0,16.40 = 13,76 gam.
→ MX = 13,76 : 0,08 = 172.
Este có dạng: R’OOC-CH=CH-COOR’’ → R’ + R’’ = 58.
Cặp thỏa mãn: R’ = 15; R’’ = 43.
→ Este X có công thức: CH3OOC-CH=CH-COOC3H7.(C8H12O4)
+) Phân tử X có 12 nguyên tử H
+) Số nguyên tử C trong T ( 4) bằng một nửa số C trong X (8)
+) Phân tử T có 1 liên kết đôi C=C và 3 liên kết π
+) Y là CH3OH, Z là C3H7OH nên không phải là đồng đẳng kế tiếp.