Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Đổi:
1,5.10-3Ci = 1,5.10-3.3,7.1010 = 55,5.106 Bq,
5mm3 = 5.10-6lít.
- Áp dụng công thức: 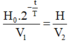
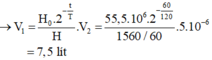

\(7,934.10^{-6}\)mol là lượng Na có trong máu người.
Bởi vì Na phân bố đều vào máu, nên giả sử thể tích máu của người là V thì:
\(\dfrac{V}{10}=\dfrac{7,934.10^{-6}}{1,5.10^{-8}}\)

Đáp án A.
Đổi 1,5.10-3Ci = 1,5.10-3.3,7.1010 = 55,5.106 Bq, 5mm3 = 5.10-6lít
Áp dụng công thức: 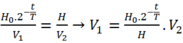
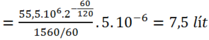

a 30
\(\omega =4\pi(rad/s)\)
\(|a|\le160\sqrt 3\) ứng với phần gạch đỏ trên hình, thời gian 1/3T ứng với véc tơ quay 1 góc 1200,.
Do vậy, mỗi một góc nhỏ là 300
\(\Rightarrow a_{max}=\dfrac{a}{\sin 30^0}=2a=320\sqrt 3(cm/s) \)
\(\Rightarrow A = \dfrac{a_{max}}{\omega^2}=2\sqrt 3(cm)\)
Cơ năng: \(W=\dfrac{1}{2}kA^2\Rightarrow k=\dfrac{2W}{A^2}=\dfrac{0,004}{(0,02\sqrt 3)^2}=...\)

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Nhận thấy: \(2,55=-13,6\cdot\left(\dfrac{1}{4^2}-\dfrac{1}{2^2}\right)\left(eV\right)\)
Suy ra nguyên tử đã nhảy từ mức n=2 lên mức n=4
Tức là, bước sóng nhỏ nhất sinh ra khi nguyên tử nhảy từ mức n=4 về n=1
Khi đó nguyên tử phát ra photon có năng lượng: \(E=-13,6\cdot\left(\dfrac{1}{4^2}-\dfrac{1}{1^2}\right)=12,75\left(eV\right)\)
\(\Rightarrow\lambda=\dfrac{hc}{E}=\dfrac{6,625.10^{-34}\cdot3.10^8}{12,75\cdot1,6.10^{-19}}=9,74.10^{-8}\left(m\right)\)
Chọn A


mik nghĩ là A . 5lit
Sau 6h lượng Na còn lại là:
$m=m_o.2^{-\dfrac{t}{T}}.$
Với: $2^{-\dfrac{-t}{T}}=2^{-\dfrac{6}{15}}=0,7579.$
$m=0,75.10^{-5}.24=1,8.10^{-4} g.$
Trong máu lấy ra có $m'=1,5.10^{-8} \left(mol\right)=3,6.10^{-7} \left(g\right).$
$V'=10 cm^3=10^{-2} \left(l\right).$
Vì tại cùng một thời điểm nên:
$\dfrac{V}{V'}=\dfrac{m}{m'} \Rightarrow V=V'\dfrac{m}{m'} \approx 5.$
Chọn $A$.