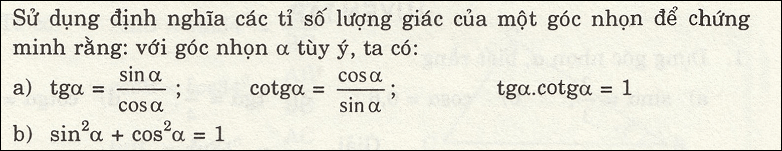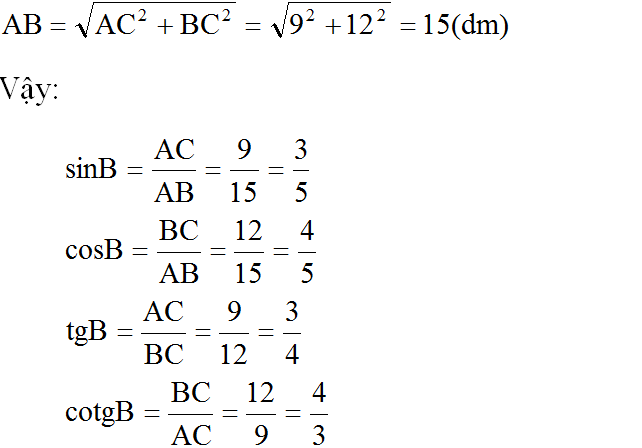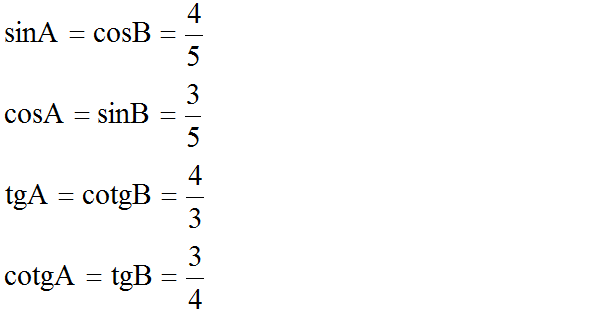K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
\(sin57^0=cos\left(90^0-57^0\right)=cos33^0\)
\(cos43^032'\) ko cần biến đổi vì góc đã thỏa mãn
\(tan72^015'=cot\left(90^0-72^015'\right)=cot\left(17^045'\right)\)
\(cot\left(85^035'\right)=tan\left(90^0-85^035'\right)=tan\left(4^025'\right)\)
19 tháng 10 2021
Bài 1:
\(\cos60^0=\sin30^0;\sin67^0=\cos23^0;\tan80^0=\cot10^0;\cot20^0=\cot20^0\)
Bài 2:
Xét tam giác ABC vuông tại A
\(a,\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{\dfrac{\sin\alpha}{\cos\alpha}}=\dfrac{\cos\alpha}{\sin\alpha}\\ \tan\alpha\cdot\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\\ b,\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(định.lí.pytago\right)\)
7 tháng 8 2020
A B C a 2a
Áp dụng định lí Pi-ta-go cho \(\Delta ABC\)vuông tại A, ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=4a^2-a^2\)
\(\Leftrightarrow AC=\sqrt{3a^2}=a\sqrt{3}\)
a) Tỉ số lượng giác của góc B là:
\(\sin B=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}\)
\(\cos B=\frac{a}{2a}=\frac{1}{2}\)
\(\tan B=\frac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\cot B=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}}\)
b) Tỉ số lượng giác của góc C là:
\(\sin C=\cos B=\frac{1}{2}\)( Định lí )
\(\cos C=\sin B=\frac{\sqrt{3}}{2}\)( Định lí )
\(\tan C=\cot B=\frac{1}{\sqrt{3}}\)( Định lí )
\(\cot C=\tan B=\sqrt{3}\)( Định lí )
Chúc bn hok tốt
B1
12 tháng 8 2017
bài 1) Bạn cần nhớ hai góc nhọn phụ nhau thì sin góc này bằng cos góc kia, tg góc này bằng cotg góc kia.
Chẳng hạn ^A + ^B = 90 độ thì sinA=cosB; tgA=cotgB.
Như vậy sin 60 độ ; cos 75 độ ; sin 52độ 30phút ; cotg 82 độ ; tg 80 độ
viết thành: cos 30độ; sin 15độ; cos 37do30phút; tg8độ; cotg 10độ.
Bài 2: dựng góc nhọn a biết
a) sina = 2/3:
- dựng góc vuông xOy và chọn 1 đoạn thẳng làm đơn vị.
- lấy A trên Ox sao cho OA=2 đơn vị độ dài
- Dựng cung trong tâm A, bán kính 3 đơn vị độ dài
cung tròn này cắt Oy tại B.
- Nối A với B, ta được góc OBA = a cần dựng.
b) cosa = 0,6 = 3/5:
- dựng góc vuông xOy và chọn 1 đoạn thẳng làm đơn vị.
- lấy A trên Ox sao cho OA=3 đơn vị độ dài
- Dựng cung trong tâm A, bán kính 5 đơn vị độ dài
cung tròn này cắt Oy tại B.
- Nối A với B, ta được góc OAB = a cần dựng.
c) tga = 3/4:
- dựng góc vuông xOy và chọn 1 đoạn thẳng làm đơn vị.
- lấy A trên Ox sao cho OA=3 đơn vị độ dài;
lấy B trên Oy sao cho OB = 4 đơn vị độ dài
- Nối A với B, ta được góc OBA = a cần dựng.
d) cotga = 3/2:
- dựng góc vuông xOy và chọn 1 đoạn thẳng làm đơn vị.
- lấy A trên Ox sao cho OA=3 đơn vị độ dài;
lấy B trên Oy sao cho OB = 2 đơn vị độ dài
- Nối A với B, ta được góc OAB = a cần dựng.
Mình cũng học lớp 9 như bạn, chúc bạn học giỏi.
30 tháng 6 2021
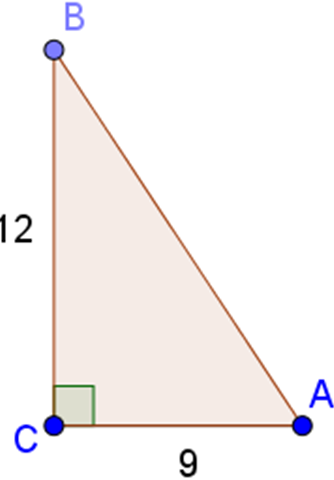
Áp dụng định lí pytago vào Δvuông ABC có:
AB²=AC²+BC²=0,9²+1,2²=2,25
⇒AB=1,5(cm)
Có góc A và góc B phụ nhau, ta có:
sin B = cosA= AC/AB = 3/5
cos B = sin A = BC/AB = 4/5
tan B = cot A = AC/BC = 3/4
cot B = tan A = BC/AC = 4/3
30 tháng 6 2021
Ta có: AC = 0,9m = 9dm; BC = 1,2m = 12dm
Theo định lí Pitago, ta có:
Vì ∠A và ∠B là hai góc phụ nhau nên suy ra:
Bạn tham khảo nha
18 tháng 10 2018
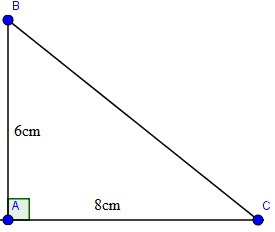
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=100BC2=AB2+AC2=62+82=100
Suy ra: BC = 10 (cm)
Ta có:
sinˆB=ACBC=810=0,8sinB^=ACBC=810=0,8
cosˆB=ABBC=610=0,6cosB^=ABBC=610=0,6
tgˆB=ACAB=86=43tgB^=ACAB=86=43
cotgˆC=tgˆB=43