Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tang của góc nhọn này và là cotg của góc nhọn kia. Giả sử α là góc nhọn của tam giác vuông có tgα = 19/28 ≈ 0,6786 , suy ra ∝ ≈ 34o10'
Vậy các góc nhọn của tam giác vuông đó có độ lớn là : α ≈ 34o10’, β ≈ 90o - 34o10’ = 55o50’

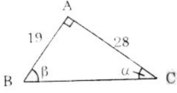
Kí hiệu góc như trên hình vẽ.
Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tg của góc nhọn này và là cotg của góc nhọn kia.
Giả sử α là góc nhọn của tam giác vuông đó.
Ta có:
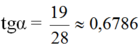
=> α ≈ 34o10'
=> β ≈ 90o - 34o10' = 55o50'
(Lưu ý: Bạn cũng có thể sử dụng cotg để tính, nhưng cũng sẽ cho kết quả tương tự bởi vì tính chất lượng giác của 2 góc phụ nhau.)

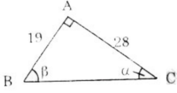
Kí hiệu góc như trên hình vẽ.
Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tg của góc nhọn này và là cotg của góc nhọn kia.
Giả sử α là góc nhọn của tam giác vuông đó.
Ta có:
![]()
= > α ≈ 34 ° 10 ' = > β ≈ 90 ° - 34 ° 10 ' = 55 ° 50 '
(Lưu ý: Bạn cũng có thể sử dụng cotg để tính, nhưng cũng sẽ cho kết quả tương tự bởi vì tính chất lượng giác của 2 góc phụ nhau.)

a/ Kẻ đường cao AH => BH là hình chiếu của AB trên BC và CH là hình chiếu của AC trên BC
Giả sử \(\frac{AB}{AC}=k\Rightarrow\frac{AB^2}{AC^2}=k^2\)
Ta có \(AB^2=BH.BC;AC^2=CH.BC\Rightarrow\frac{AB^2}{AC^2}=\frac{BH}{CH}=k^2\)
b/ Áp dụng câu A sẽ tính được tỷ số hình chiếu 2 cạnh góc vuông trên BC là mà biết chiều dài BC=82 bài toán là dạng tìm 2 số khi biết tổng và tỷ ở lớp 5 rồi bạn tự giải nốt nhé

Gọi độ dài của tam giác vuông là x. Điều kiện x > 0.
Tỉ số giữa cạnh huyền và một cạnh góc vuông sẽ là x/15.
Theo bài ra ta có :
x/15=13/12 (=) 12x=13*15 (=) 12x = 195 (=) x=16,25
Vậy độ dài cạnh huyền là 16,25 cm
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)