Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Tại M cách vân trung tâm 1 mm người ta quan sát được vân sáng bậc 2 tức là: 2i = 1mm => i =0,5 mm dọc theo đường thẳng vuông góc với mặt phẳng chứa hai khe một đoạn 50/3 cm thì khoảng vân mới là:
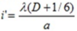
M chuyển thành vân tối bậc 2 tức là: 2i = 1,5 i' => i' = 2/3 mm
=> Δi = 1/6 mm
Khi dời màn ra xa thêm 1/6 mm thì khoảng vân tăng thêm 1/6mm tức là:
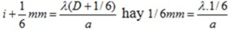
=> λ = 0,50 μm

Cách giải:
Khi dịch chuyển màn ra xa thì khoảng vân sẽ tăng do vậy bậc của vân sẽ giảm xuống, M trở thành vân tối hai lần thì lần cuối cùng ứng với vân tối bậc 4, ta có:
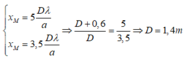
Thay vào phương trình thứ nhất

Đáp án A

Phương pháp giải : Sử dụng lý thuyết về giao thoa sóng ánh sáng
Cách giải:
Ban đầu tại M có vân sáng bậc 4
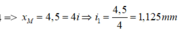
Sau khi dịch mà ra xa => D tăng => i tăng => M chuyển thành vân tối thứ 2 khi đó x M = 2 , 5 i 2 thì khoảng dịch là 0,9m
Ta có:
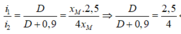
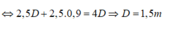
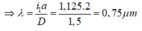
=> Chọn B

Chọn C
M cách vân trung tâm 1,2 mm người ta quan sát được vân sáng bậc 4 tức là:
xM = 4i và 4i = 1,2 mm => i = 0,03 mm
di chuyển từ từ màn quan sát ra xa và dọc theo dường thẳng vuông góc với mặt phẳng chứ hai khe thì thấy tại M chuyển thành vân sáng bậc ba tức là:
xM = 3i'
=> 3i' = 4i => i' = 0,4 mm
=> Δi = i' - i = 0,1 mm
Khi dời màn ra xa thêm 0,25 m thì khoảng vân tăng thêm 0,1 mm tức là:
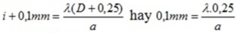
=> λ = 0,40 μm

Cách giải: Đáp án C
Từ giải thuyết ta có hai trường hợp
Nều giảm khoang cách từ hai khe đến màn quan sát ta có
![]()
![]()
Nếu tăng khoảng cách từ hai khe tới màn quan sát ta có
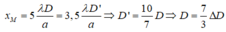
![]()
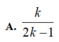
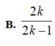
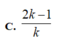




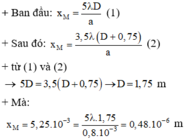
Phương pháp:
Áp dụng lí thuyết về giao thoa sóng ánh sáng, công thức tính khoảng vân i = λD/a
Cách giải:
+ Khi chưa dịch màn M:
+ Khi dịch màn M ra xa một đoạn 40 cm:
Từ (1) và (2) ta có:
+ Khi dịch màn M lại gần một đoạn 40 cm:
Từ (1) và (3) ta có:
Vậy tại M có vân sáng bậc 3
Chọn A