TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 8
Gọi x(cm) là chiều rộng của hình hộp chữ nhật
(Điều kiện: x>0)
Chiều dài của hình hộp chữ nhật là: \(x:80\%=1,25x\left(\operatorname{cm}\right)\)
Diện tích xung quanh của hình hộp chữ nhật là:
\(\left(x+1,25x\right)\cdot2\cdot25=50\cdot2,25x=112,5x\left(\operatorname{cm}^2\right)\)
Diện tích toàn phần của hình hộp chữ nhật là:
\(112,5x+2\cdot x\cdot1,25x=2,5x^2+112,5x\left(\operatorname{cm}^2\right)\)
Theo đề, ta có:
\(2,5x^2+112,5x=8500\)
=>\(x^2+45x=3400\)
=>\(x^2+45x-3400=0\)
=>(x+85)(x-40)=0
=>\(\left[\begin{array}{l}x=-85\left(loại\right)\\ x=40\left(nhận\right)\end{array}\right.\)
=>Chiều rộng là 40cm; Chiều dài là \(40\cdot1,25=50\left(\operatorname{cm}\right)\)
Diện tích xung quanh là \(112,5\cdot40=4500\left(\operatorname{cm}^2\right)\)
NL
1
AD
20 tháng 8 2023
Kẻ Az//Bx//Dy
=> BAD = BAz + DAz = (180o - ABx) + (180o - ADy) = 30o + 60o = 90o
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
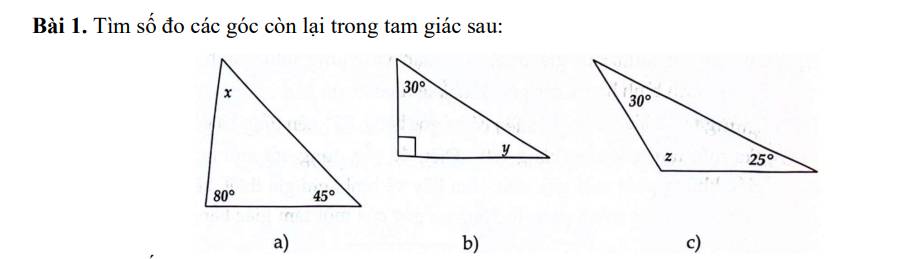
Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
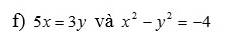
\(A=-\dfrac{1}{6}-\left[\dfrac{9}{16}-\dfrac{9}{8}+\dfrac{3}{4}\right]\)
\(=\dfrac{-1}{6}-\dfrac{9-18+12}{16}=\dfrac{-1}{6}-\dfrac{3}{16}\)
\(=\dfrac{-8}{48}-\dfrac{9}{48}=-\dfrac{17}{48}\)