
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

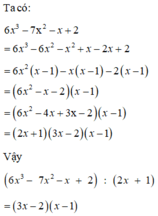

a) (-x2 +6x3 - 26x + 21) : (3-2x)
= -3x2 + 5x + 11/2 ( dư 37/1/2)
b) (2x4 - 13x3 - 15 + 5x + 21x2) : (4x-x2 -3)
= -2x2 + 5x + 5

\(\left(x^3y+xy^3+xy\right):y\left(x^2+y^2+1\right).\)
\(=xy.\left(x^2+y^2+1\right):y.\left(x^2+y^{2+}1\right)\)
\(=\left(xy:y\right).\left(x^2+y^2+1\right)^2\)
\(=x.\left(x^2+y^2+1\right)^2\)

\(\frac{3\left(x+1\right)}{x+2}-\frac{3x-6}{x^2-4}\)
\(=\frac{3\left(x+1\right)}{x+2}-\left(\frac{3x-6}{x^2-4}\right)\)
\(=\frac{3x^2-6x^2-12x+24}{x^3+2x^2-4x-8}\)
\(=\frac{3\left(x+2\right)\left(x-2\right)\left(x-2\right)}{\left(x+2\right)\left(x+2\right)\left(x-2\right)}\)
\(=\frac{3x-6}{x+2}\)
\(\frac{x^2+4x+4}{1-x}.\frac{\left(1-x\right)^2}{3\left(x+2\right)^3}\)
\(=\frac{x^2+4x+4}{1-x}.\left[\frac{\left(1-x\right)^2}{3\left(x+2\right)^3}\right]\)
\(=\frac{x^4+2x^3-3x^2-4x+4}{-3x^4-15x^3-18x^2+12x+24}\)
\(=\frac{\left(x-1\right)\left(x-1\right)\left(x+2\right)\left(x+2\right)}{3\left(-x+1\right)\left(x+2\right)\left(x+2\right)\left(x+2\right)}\)
\(=\frac{-x+1}{3x+6}\)

a. \(=\frac{x+1}{2.\left(x+3\right)}+\frac{2x+3}{x.\left(x+3\right)}=\frac{x^2+x+4x+6}{2x.\left(x+3\right)}=\frac{x^2+5x+6}{2x.\left(x+3\right)}=\frac{\left(x+2\right).\left(x+3\right)}{2x.\left(x+3\right)}=\frac{x+2}{2x}\)
b. =\(\frac{2.\left(x+3\right)}{x.\left(3x-1\right)}.\frac{-\left(3x-1\right)}{x.\left(x+3\right)}=\frac{-2}{x^2}\)
Chắc chắn đúng, mik nhaaaaaa

cái này có mẫu thức chung là 3(x-1) rồi bạn quy đồng lên là được thôi

Tú mà không làm được câu này á :))
( x - 6 )( x - 7 )( x - 8 )( x - 9 ) - 8
= [ ( x - 6 )( x - 9 ) ][ ( x - 7 )( x - 8 ) ] - 8
= ( x2 - 15x + 54 )( x2 - 15x + 56 ) - 8 (*)
Đặt t = x2 - 15x + 54
(*) <=> t( t + 2 ) - 8
= t2 + 2t - 8
= ( t - 2 )( t + 4 )
= ( x2 - 15x + 52 )( x2 - 15x + 58 )
=> [ ( x - 6 )( x - 7 )( x - 8 )( x - 9 ) - 8 ] : ( x2 - 15x + 100 )
= ( x2 - 15x + 52 )( x2 - 15x + 58 ) : ( x2 - 15x + 100 )
Đặt y = x2 - 15x + 100
Ta có được phép chia ( y - 48 )( y - 42 ) : y
= y2 - 90y + 2016 : y
= [ ( x2 - 15x + 100 )2 - 90( x2 - 15x + 100 ) + 2016 ] : ( x2 - 15x + 100 )
Đến đây thì quá dễ rồi :)) dư 2016 nhá

\(\frac{x^2-3x-x+3}{x-3}=\frac{x\left(x-3\right)-\left(x-3\right)}{x-3}=\frac{\left(x-3\right)\left(x-1\right)}{x-3}=x-1\)( ĐK: \(x\ne3\))
\(\frac{2x^3-5x^2-4x+3}{2x-1}=\frac{\left(2x^3-x^2\right)-\left(4x^2-2x\right)-\left(6x-3\right)}{2x-1}=\frac{x^2\left(2x-1\right)-2x\left(2x-1\right)-3\left(2x-1\right)}{2x-1}=\frac{\left(2x-1\right)\left(x^2-2x-3\right)}{2x-1}=x^2-2x-3\)( ĐK: \(x\ne\frac{1}{2}\))
Tham khảo nhé~

2\(\frac{2}{x-1}-\frac{7-x}{3x-3}=\frac{2}{x-1}-\frac{7-x}{3\left(x-1\right)}=\frac{6}{3\left(x-1\right)}-\frac{7-x}{3\left(x-1\right)}=\frac{13-x}{3\left(x-1\right)}\)