Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{r}{r_0}=\frac{2,2.10^{-10}}{5,3.10^{-11}} \approx 4.\)
=> \(r = 4r_0 = 2^2 r_0.\) Tức là electron nhảy lên trạng thái dừng L (n = 2).

- Trạng thái kích thích thứ 3 ứng với quỹ đạo dừng N (K,L,M,N).
- Tức là n = 4. Vậy bán kính là :
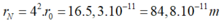

Đáp án C
Phương pháp: Sử dụng lí thuyết về trạng thái dừng của nguyên tử hiđrô
Cách giải:
Áp dụng công thức
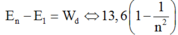
![]()
=> electron nhận thêm một lượng động năng để chuyển lên quỹ đạo ứng với n = 3
Bán kính quỹ đạo tăng thêm một lượng
![]()
![]()
Chọn C

\(r_n=n^2r_0.\)
Bán kính quỹ đạo dừng N ứng với n = 4
\(r_N=r_4= 4^2r_0=16r_0.\)
Bán kính quỹ đạo dừng L ứng với n = 2
\(r_L=r_2= 2^2r_0=4r_0.\)
Như vậy khi electron chuyển từ quỹ đạo N về quỹ đạo L thì bán kĩnh quỹ đạo giảm
\(\Delta r= r_4-r_2= 16r_0-4r_0= 12r_0.\)
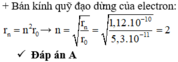
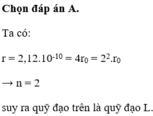
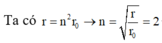
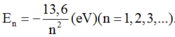
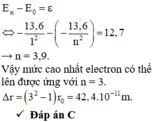
Chọn đáp án D
Bán kính quỹ đạo dừng của electron r n = n 2 r 0 , quỹ đạo dừng M ứng với n = 3 → r M = 9 r 0