Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:
DE // AB và DE = 1/2 AB (1)
IK // AB và IK = 1/2 AB (2)
Từ (1) và (2) suy ra:
DE // IK và DE = IK.

Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD


Giải
a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 vào ∆ABC và ∆AGB ta có:
DE // AB và DE=1/2AB (1)
IK // AB và IK=1/2AB (2)
Từ (1) và (2) suy ra: DE // IK và DE = IK
b) AD và BE là 2 đường trung tuyến của ∆ABC cắt nhau tại G.
⇒AG=2/3AD(tính chất đường trung tuyến)
Bài này dễ mà
Sử dụng tính chất đường trung tuyến của tam giác rồi CM tam giác IGK = tam giác DGE
=> IK=DE ( 2 cạnh tương ưng )
=> GIK = GDE ( 2 góc tương ứng)
Mà GIK và GDE là 2 góc so le trong
=> ....... (các bạn tự Cm nhé, Mình chỉ gợi ý như thế thôi )
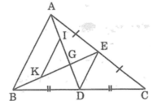
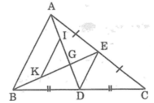
a) DE // AB, DE = \(\dfrac{1}{2}\)AB, IK // AB, IK = \(\dfrac{1}{2}\)AB
=> DE//IK và DE = IK
b) Xét tg GDE và tg GIK có:
DE = IK (cmt)
GDE = GIK (slt)
GED = GKI (slt)
=> tg GDE = tg GIK (g.c.g)
=> GD = GI ( c.t.ứ)
Có GD = GI = IA nên AG = \(\dfrac{2}{3}\)AD
có hình ko bn