Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Chọn B
Nếu S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox thì thể tích của vật thể giới hạn bởi hai mặt phẳng x = a và x = b là
V = ∫ a b S x d x

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

19.
\(\overline{z}=1-3i\)
\(\Rightarrow u=\left(1-3i\right)\left(2-i\right)=2+3i^2-7i=-1-7i\)
Phần ảo bằng -7
20.
Tọa độ G: \(\left\{{}\begin{matrix}x_G=\frac{x_A+x_B+x_C}{3}=2\\y_G=\frac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)
Biểu diễn trên mặt phẳng phức: \(z=2+i\)
21.
Đề đúng là \(\left(1-i\right)+44\overline{z}=7-7i\) chứ?
\(\Rightarrow44\overline{z}=6-6i\Rightarrow\overline{z}=\frac{3}{22}-\frac{3}{22}i\)
\(\Rightarrow z=\frac{3}{22}+\frac{3}{22}i\Rightarrow\left|z\right|=\sqrt{\left(\frac{3}{22}\right)^2+\left(\frac{3}{22}\right)^2}=\frac{3\sqrt{2}}{22}\)
15.
Diện tích thiết diện:
\(S=\frac{1}{2}\left(2\sqrt{1-x^2}\right)^2=2\left(1-x^2\right)=2-2x^2\)
Thể tích:
\(S=\int\limits^1_{-1}\left(2-2x^2\right)dx=\frac{8}{3}\)
16.
\(z=z'\Leftrightarrow\left\{{}\begin{matrix}a=c\\b=d\end{matrix}\right.\) (phần thực bằng phần thực, phần ảo bằng phần ảo)
17.
\(\overline{z}=3+2i\Rightarrow\) phần ảo là 2 (không phải 2i đâu)
18.
\(z=3+2i\Rightarrow z^2=\left(3+2i\right)^2=9+4i^2+12i=5+12i\)
\(\Rightarrow\) phần thực bằng 5

Bài 14:
Vecto chỉ phương của đường thẳng $d$ là: $\overrightarrow{u_d}=(1; -1; 2)$
Mp $(P)$ vuông góc với $d$ nên nhận $\overrightarrow{u_d}$ là vecto pháp tuyến
Do đó PTMP $(P)$ là:
$1(x-x_M)-1(y-y_M)+2(z-z_M)=0$
$\Leftrightarrow x-y+2z=0$
Đáp án A
Bài 13:
Khi quay tam giác đều ABC quanh cạnh AB thì ta thu được một khối hình là hợp của 2 hình nón (ngược chiều nhau) có cùng bán kính đáy $r$ là đường cao của tam giác đều, tức là $r=\frac{\sqrt{3}}{2}.1=\frac{\sqrt{3}}{2}$ và đường cao là $h=\frac{AB}{2}=\frac{1}{2}$
Thể tích 1 hình nón: $V_n=\frac{1}{3}\pi r^2h=\frac{\pi}{8}$
Do đó thể tích của khối hình khi quay tam giác đều ABC quanh AB là: $2V_n=\frac{\pi}{4}$

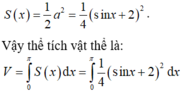
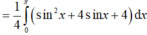
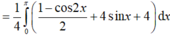
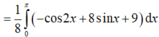
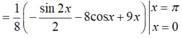
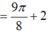

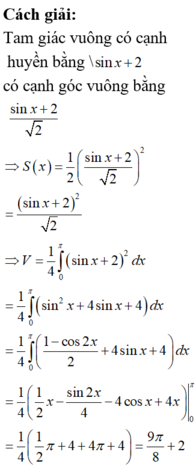

Đáp án C
Do thiết diện là một tam giác đều nên diện tích thiết diện là: