
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


– Phương trình (a) có tập nghiệm là S1
Phương trình (b) có tập nghiệm là S2
Nếu S1 ⊂ S2 thì ta nói (b) là phương trình hệ quả của phương trình (a), kí hiệu: (a) ⇒ (b)
– Ví dụ : Phương trình x + 1 = 0 có tập nghiệm là S1 = {–1}
phương trình x2 – x – 2 = 0 có tập nghiệm là S2 = {–1; 2}
Ta có: S1 ⊂ S2 nên phương trình x2 – x – 2 = 0 là phương trình hệ quả của phương trình x + 1 = 0, kí hiệu:
x + 1 = 0 ⇒ x2 – x – 2 = 0.

Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Hai phương trình \(2x-5=0\)và \(3x-\dfrac{15}{2}=0\) tương đương với nhau vì cùng có nghiệm duy nhất \(x=\dfrac{5}{2}\)
Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Nếu f(x) = g(x) tương đương với f1(x) = g1(x) thì ta viết:
f(x) = g(x)  f1(x) = g1(x)
f1(x) = g1(x)
Ví dụ:
|
Hai phương trình 2x - 5 = 0 và
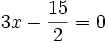 tương đương với nhau vì cùng có nghiệm duy nhất tương đương với nhau vì cùng có nghiệm duy nhất 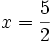 . . |
| |

- Hai phương trình có cùng tập nghiệm thì tương đương nhau.
- Ví dụ hai phương trình:
x2 - 3x + 2 = 0 và (x - 1)(x - 2)(x2 + x + 1) = 0
là hai phương trình tương đương vì chúng có cùng tập nghiệm là {1, 2}.

a) Ví dụ:
\(\begin{array}{l}{x^2} - x + 1 > 0\\ - {x^2} + 5x + 5 \le 0\end{array}\)
b)
Bất phương trình bậc nhất: \(x - 1 > 0\)
Bất phương trình hai ẩn: \(2x + y < 5\)

a) \(\left\{ \begin{array}{l}3x + y - 1 \le 0\\2x - y + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + 0 - 1 = - 1 \le 0\\2.0 - 0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((0; - 1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + ( - 1) - 1 = - 2 \le 0\\2.0 - ( - 1) + 2 = 3 \ge 0\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y - 1 < 0\\x + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((1;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\1 + 2 = 3 \ge 0\end{array} \right.\)
d) \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 0 - 3 = - 3 \le 0\\ - 2.0 + 0 + 3 = 3 \ge 0\\0 \ge 0\\0 \ge 0\end{array} \right.\)
Cặp số \((0;1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 1 - 3 = - 2 \le 0\\ - 2.0 + 1 + 3 = 4 \ge 0\\0 \ge 0\\1 \ge 0\end{array} \right.\)

Ta có 2 x 2 − x = 0 ⇔ x = 0 x = 1 2
Do đó, tập nghiệm của phương trình đã cho là S 0 = 0 ; 1 2
Xét các đáp án:
Đáp án A. Ta có:
2 x − x 1 − x = 0 ⇔ 1 − x ≠ 0 2 x ( 1 − x ) − x = 0 ⇔ x ≠ 1 x = 0 x = 1 2 ⇔ x = 0 x = 1 2
Do đó, tập nghiệm của phương trình là S 1 = 0 ; 1 2 ⊃ S 0
Đáp án B. Ta có: 4 x 3 - x = 0 ⇔ x = 0 x = ± 1 2
Do đó, tập nghiệm của phương trình là S 2 = − 1 2 ; 0 ; 1 2 ⊃ S 0
Đáp án C. Ta có: 2 x 2 - x 2 + x - 5 2 = 0 ⇔ 2 x 2 − x = 0 x − 5 = 0 ⇔ 2 x 2 − x = 0 x = 5 (vô nghiệm)
Do đó, phương trình vô nghiệm nên không phải hệ quả của phương trình đã cho.
Đáp án D. Ta có: 2 x 3 + x 2 - x = 0 ⇔ x = 0 x = 1 2 x = − 1
Do đó, tập nghiệm của phương trình là S 2 = − 1 ; 0 ; 1 2 ⊃ S 0
Đáp án cần chọn là: C

2x + 3 ≥ -6
Vế trái của bất phương trình: 2x + 3
Vế phải của bất phương trình: -6

Phương trình một ẩn: 2x + 4 = 0
Phương trình hai ẩn: 3x + 7y = 10

+ Mệnh đề đảo của mệnh đề A ⇒ B là mệnh đề B ⇒ A.
+ Nếu mệnh đề A ⇒ B đúng thì mệnh đề B ⇒ A có thể đúng hoặc sai.
Ví dụ:
+ Mệnh đề A: “ΔABC là tam giác đều”.
Mệnh đề B: “ΔABC có AB = BC = CA”
Mệnh đề A ⇒ B là mệnh đề đúng và mệnh đề B ⇒ A cũng là mệnh đề đúng.
+ Mệnh đề A: “ΔABC là tam giác đều”
Mệnh đề B: “ΔABC có AB = BC ”
Mệnh đề A ⇒ B là mệnh đề đúng nhưng mệnh đề B ⇒ A sai.
Nếu mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình f1(x) = g1(x) thì phương trình
f1(x) = g1(x) được gọi là phương trình hệ quả của phương trình f(x) = g(x).
Ta viết f(x) = g(x) f1(x) = g1(x).
f1(x) = g1(x).
Ví dụ: Giải phương trình:
Giải
Điều kiện của phương trình (4) là x ≠ 0 và x ≠ 1.
Nhân hai vế của phương trình (4) với x(x - 1) ta được phương trình hệ quả:
(4) x + 3 + 3(x - 1) = x(2 - x)
x + 3 + 3(x - 1) = x(2 - x)
Phương trình cuối cùng có hai nghiệm là x = 0 và x = -2.
Ta thấy x = 0 không thỏa mãn điều kiện của phương trình (4), đó là nghiệm ngoại lai, nên bị loại. Còn lại x = -2 thỏa mãn điều kiện và thỏa mãn phương trình (4).
Vậy phương trình (4) có nghiệm duy nhất là x = -2.
Nếu mọi nghiệm của phương trình \(f\left(x\right)=g\left(x\right)\) đều là nghiệm của phương trình \(f_1\left(x\right)=g_1\left(x\right)\)thì phương trình
\(f_1\left(x\right)=g_1\left(x\right)\) được gọi là phương trình hệ quả của phương trình \(f\left(x\right)=g\left(x\right)\)