Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(y=-f\left(x\right)\) đồng biến trên khoảng \(\left(a;b\right)\)

Trục đối xứng của hàm số là: \(x = \frac{5}{2}.\)
Vì \(a = 1 > 0\) nên hàm số đồng biến trên khoảng \(\left( {\frac{5}{2}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;\frac{5}{2}} \right).\)
Chọn C.

Do hàm số y = f(x) nghịch biến trên khoảng (a;b) nên
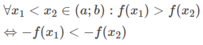
Vậy hàm số y = - f(x) đồng biến trên khoảng (a;b).

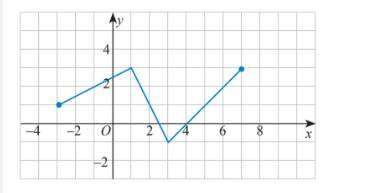
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá
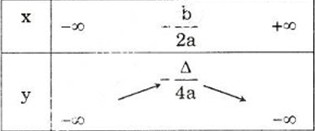
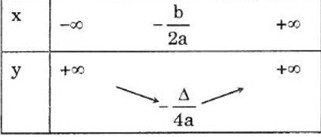
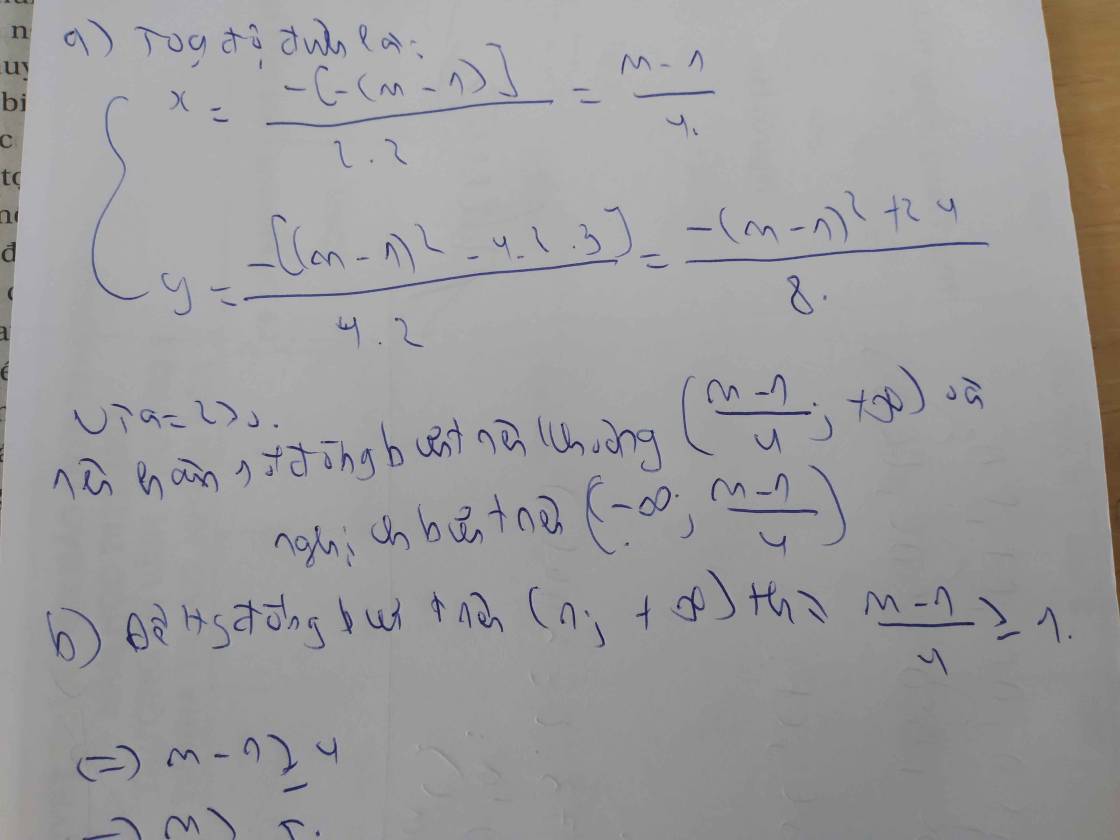

Cho hàm số y = f(x) xác định trên khoảng (a; b).
+ Hàm số y = f(x) đồng biến trên khoảng (a; b) nếu:
x1 < x2 ⇔ f(x1) < f(x2) ∀ x1, x2 ∈ (a; b)
+ Hàm số y = f(x) nghịch biến trên khoảng (a; b) nếu:
x1 < x2 ⇔ f(x1) > f(x2) ∀ x1, x2 ∈ (a; b)