Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Ví dụ: ΔABC sau khi thực hiện phép quay tâm C, góc 90º rồi lấy đối xứng qua d được ΔA1B1C1.
⇒ ΔABC = ΔA1B1C1
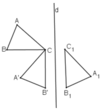
+ Hai hình được gọi là đồng dạng nếu có một phép đồng dạng biến hình này thành hình kia.
Ví dụ: ΔABC sau khi thực hiện liên tiếp phép quay tâm C góc 90º; đối xứng qua đường thẳng d và phép vị tự tâm B tỉ số 1,5 được ΔA1B1C1
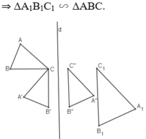

-Hai thanh sắt đối diện nhau ở hai bên cầu song song với nhau.
-Hai thanh sắt liền nhau cùng nằm ở thành cầu hoặc mái cầu cắt nhau.
-Thanh sắt nằm ở mái cầu và thanh sắt nằm ở thành cầu chéo nhau.

Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau

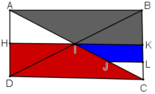
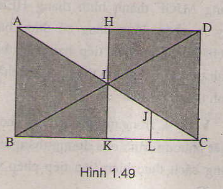
+ I là trung điểm AC; BD; HK
⇒ ĐI(H) = K ; ĐI(D) = B ; ĐI (C) = A.
⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)
+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA
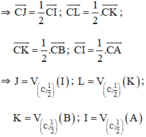
⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số 1/2.
⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số 1/2.
⇒ IJKI và IHDC đồng dạng.

a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
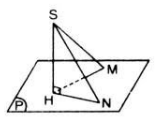
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.

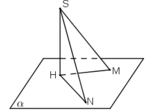
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .

tham khảo
Trong không gian, hai đường thẳng vuông góc với nhau là hai đường thẳng nằm trong hai mặt phẳng vuông góc với nhau
Hai đường thẳng vuông góc với nhau là hai đường thẳng nằm trong 2 mp vuông góc với nhau

- Phép biến hình:
Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M\' của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng. Nếu kí hiệu phép biến hình đó là F thì ta viết F(M) = M\' hay M\' = F(M) và gọi điểm M\' là ảnh của điểm M hay M là điểm tạo ảnh của M\' qua phép biến hình F.
- Phép dời hình:
Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nghĩa là với hai điểm M, N tùy ý và ảnh M', N' tương ứng của chúng, ta luôn có M'N'=MN.
- Phép đồng dạng:
Phép biến hình f được gọi là phép đồng dạng tỉ số k, (k>0), nếu với hai điểm M, N bất kì và ảnh M\', N\' tương ứng của chúng, ta luôn có M\'N\' = kMN.
Mối liên hệ: Phép dời hình là trường hợp riêng của phép đồng dạng với tỉ số k = 1.
- Phép biến hình:
Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M\' của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng. Nếu kí hiệu phép biến hình đó là F thì ta viết F(M) = M' hay M' = F(M) và gọi điểm M' là ảnh của điểm M hay M là điểm tạo ảnh của M\' qua phép biến hình F.
- Phép dời hình:
Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nghĩa là với hai điểm M, N tùy ý và ảnh M', N' tương ứng của chúng, ta luôn có M'N'=MN.
- Phép đồng dạng:
Phép biến hình f được gọi là phép đồng dạng tỉ số k, (k>0), nếu với hai điểm M, N bất kì và ảnh M', N' tương ứng của chúng, ta luôn có M'N' = kMN.
Mối liên hệ: Phép dời hình là trường hợp riêng của phép đồng dạng với tỉ số k = 1.


Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.