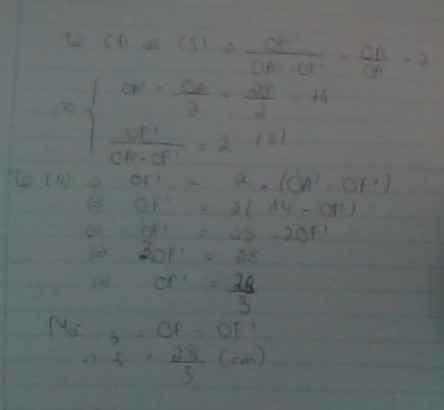Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\)
\(\Rightarrow d'=4,8cm\)
Độ cao ảnh A'B':
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{8}{4,8}\Rightarrow h'=1,2cm\)

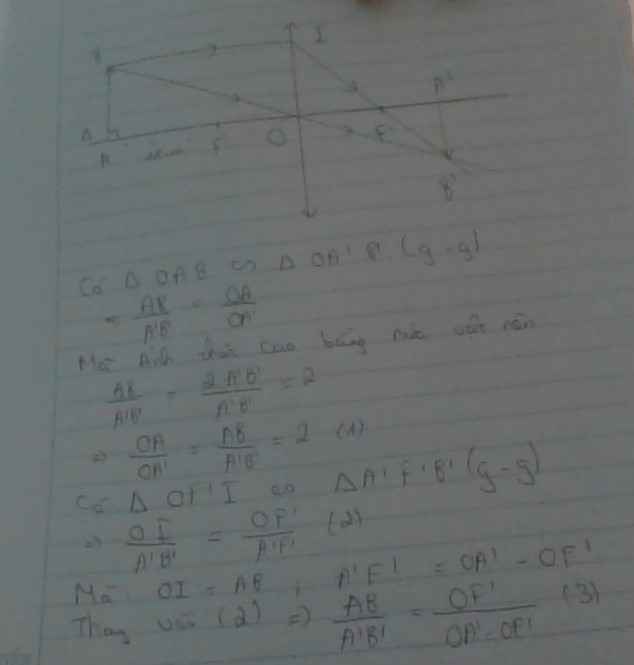
Vật sáng đặt ngoài tiêu cự vậy qua thấu kính hội tụ cho một ảnh thật, ngược chiều với vật như hình vẽ:
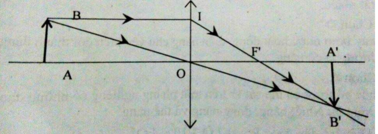
∆ ABO ~ ∆ A’B’O => AB/A'B' = OA/OA' (1)
∆ OIF’ ~ ∆ A’B’F’ => OI/A'B' = OF'/F'A' (2)
Và OI = AB nên từ (1) (2) suy ra:
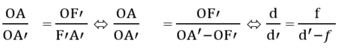
30/d' = 15/(d'-15 ) giải ra ta được d’ = 30cm. Vậy ảnh thật cách thấu kính 30cm.

Đáp án D
Hình vẽ và lập luận dựa vào ∆ đồng dạng, ta có ảnh ở đây là ảnh ảo và chứng minh được:
=> d/d' = f/(f+d') ⇔ 8/d' = 12/(12+d')
12d’ = 8d’ + 96 ⇔ 4d’ = 96 ⇔ d’ = 24 (cm)
Vậy ảnh là ảo và thấu kính cách d’ = 24 (cm).

Đáp án D
Hình vẽ và lập luận dựa vào ∆ đồng dạng ta có:
d/d' = f/(f-d') ⇔ d/36 = 12/(36-12) = 1/2
d = 18 (cm)

Đáp án B
Hình vẽ như câu 13 và lập luận ta có: d/d' = f/(f-d') ⇔ d/20 = 10/(20-10) = 1
d = 20 (cm). Vậy vật đặt cách thấu kính d = 20 (cm)

Đáp án B
Tương tự từ ∆ đồng dạng ta được công thức:
d/d' = f/(f+d')
⇔ d/24 = 12/(12+24) = 1/3
d = 24/3 = 8 (cm)

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{30}+\dfrac{1}{d'}\)
\(\Rightarrow d'=20cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{1}{h'}=\dfrac{30}{20}\Rightarrow h'=\dfrac{2}{3}cm\)