
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
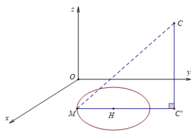
Gọi \(B=(a,0,0)\) và \(C=(b,0,0)\)
Ta có \(BC=\sqrt{(a-b)^2}=6=|a-b|\) \((1)\)
Vì \(B,C\) nằm trên mặt cầu nên :
\(R=AB=AC\Leftrightarrow \sqrt{(a-1)^2+25}=\sqrt{(b-1)^2+25}\Leftrightarrow (a-1)^2=(b-1)^2\)
\(\Leftrightarrow (a-b)(a+b-2)=0\Leftrightarrow a+b=2\) \((2)\)vì \(a-b\neq 0\)
Từ \((1),(2)\Rightarrow \)\(\left[\begin{matrix}\left\{\begin{matrix}a=4\\b=-2\end{matrix}\right.\\\left\{\begin{matrix}a=-2\\b=4\end{matrix}\right.\end{matrix}\right.\). Từ đây thu được \(R=\sqrt{34}\)
Vậy PTMC là \((x-1)^2+(y-4)^2+(z-3)^2=34\)

Đáp án B.
Ta có:
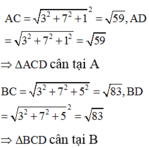
Từ đó gọi M là trung điểm của CD ta có ![]()
Do đó chu vi ∆ A B M là
![]()
(vì AB không thay đổi), tức là khi M là trung điểm cuả CD hay M(0;1;-1)

\(PC=2SP\Rightarrow SP=\dfrac{1}{3}SC\)
\(\dfrac{V_{SMNP}}{V_{SABC}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}.\dfrac{SP}{SC}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{3}=\dfrac{1}{12}\)

\(y'=x^2-\left(3m+2\right)x+2m^2+3m+1\)
\(\Delta=\left(3m+2\right)^2-4\left(2m^2+3m+1\right)=m^2\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{3m+2+m}{2}=2m+1\\x_2=\frac{3m+2-m}{2}=m+1\end{matrix}\right.\)
Để hàm số có cực đại, cực tiểu \(\Rightarrow x_1\ne x_2\Rightarrow m\ne0\)
- Nếu \(m>0\Rightarrow2m+1>m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=m+1\\x_{CT}=2m+1\end{matrix}\right.\)
\(\Rightarrow3\left(m+1\right)^2=4\left(2m+1\right)\) \(\Rightarrow3m^2-2m-1=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-\frac{1}{3}< 0\left(l\right)\end{matrix}\right.\)
- Nếu \(m< 0\Rightarrow m+1>2m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=2m+1\\x_{CT}=m+1\end{matrix}\right.\)
\(\Rightarrow3\left(2m+1\right)^2=4\left(m+1\right)\Rightarrow12m^2+8m-1=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\frac{-2+\sqrt{7}}{6}>0\left(l\right)\\m=\frac{-2-\sqrt{7}}{6}\end{matrix}\right.\) \(\Rightarrow\sum m=\frac{4-\sqrt{7}}{6}\)


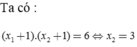
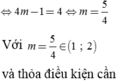



😭😭😭😭😭😭😭😭😭😭😭