


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) Cả tử số và mẫu số của \(\frac{7n^2-3n+12}{n^2+2n+2}\) đều dẫn đến \(\infty\) nên không thể trả lời ngay biểu thức đó tiến đến giới hạn nào (dạng vô định \(\left(\frac{\infty}{\infty}\right)\)). Tuy nhiên sau khi chia cả tử số và mẫu số cho \(n^2\) :
\(\frac{7n^2-3n+12}{n^2+2n+2}=\frac{7-\frac{3}{n}+\frac{12}{n^2}}{1+\frac{2}{n}+\frac{2}{n^2}}\)
Ta thấy ngay tử số gần đến 7 và mẫu số gần đến 1 (vì \(\lim\limits\frac{1}{n^p}=0,p\ge1\)
Điều đó cho phép ta áp dụng công thức và thu được kết quả \(\lim\limits\frac{7n^2-3n+12}{n^2+2n+2}=\lim\limits\frac{7-\frac{3}{n}+\frac{12}{n^2}}{1+\frac{2}{n}+\frac{2}{n^2}}=7\)
b) Áp dụng công thức "Nếu tồn tại \(\lim\limits a^n,k\in\)N* thì tồn tại \(\lim\limits\left(a_n\right)^k=\left(\lim\limits a_n\right)^k\)"
ta có :
\(\lim\limits a_n=\left[\lim\limits\left(\frac{3n^2+n-2}{4n^2+2n+7}\right)\right]^3\)
Mặt khác do \(\lim\limits\frac{3n^2+n-2}{4n^2+2n+7}=\lim\limits\frac{3+\frac{1}{n}-\frac{2}{n^2}}{4+\frac{2}{n}+\frac{7}{n^2}}=\frac{3}{4}\)
nên \(\lim\limits a_n=\left(\frac{3}{4}\right)^3=\frac{27}{64}\)

a) lim (n3 + 2n2 – n + 1) = lim n3 (1 + ) = +∞
b) lim (-n2 + 5n – 2) = lim n2 ( -1 + ) = -∞
c) lim ( - n) = lim
= lim = lim
= lim
=
.
d) lim ( + n) = lim (
+ n) = lim n (
+ 1) = +∞.

\(\lim\limits\left(\sqrt{2n^2+3}-\sqrt{n^2+1}\right)=\lim\limits\frac{n^2-2}{\left(\sqrt{2n^2+3}+\sqrt{n^2+1}\right)}=\lim\limits\frac{n-\frac{2}{n}}{\sqrt{2+\frac{3}{n^2}}+\sqrt{1+\frac{1}{n^2}}}=+\infty\)
\(\lim\limits\frac{1}{\sqrt{n+1}-\sqrt{n}}=\lim\limits\left(\sqrt{n+1}+\sqrt{n}\right)=+\infty\)

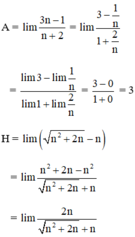
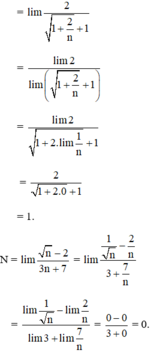
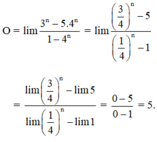
Khi thay đổi chữ số 1530 bởi các biểu thức giới hạn tương ứng ta được chữ HOAN là tên các bạn học sinh đã cho.

\(limu_n=lim\dfrac{1}{n}=0\); \(limv_n=lim\left(-\dfrac{1}{n}\right)=0\).
\(limf\left(u_n\right)=lim\left(\sqrt{\dfrac{1}{n}}+1\right)=1\).
\(limf\left(v_n\right)=lim\left(2.\dfrac{-1}{n}\right)=lim\dfrac{-2}{n}=0\).
Hai dãy số \(\left(u_n\right)\) và \(\left(v_n\right)\) đều có giới hạn 0 khi n tiến ra dương vô cùng nhưng \(limf\left(u_n\right)\ne limf\left(v_n\right)\) nên f không có giới hạn tại \(x=0\).