OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
7 tháng 1 2017
Cho phương trình sau:  sin   3 x - sin   x + cos   2 x = 1 . Phương trình có họ nghiệm  x = π a + k 2 π 3 ,   k ∈ ℤ  hỏi giá trị của a  A. 1 B. 6 C. 3 D. 4...
Đọc tiếp

Cho phương trình sau:  sin   3 x - sin   x + cos   2 x = 1 . Phương trình có họ nghiệm  x = π a + k 2 π 3 ,   k ∈ ℤ  hỏi giá trị của a 

A. 1

B. 6

C. 3

D. 4
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
7 tháng 1 2017

Đáp án đúng : B

Đúng(0)
PT
Pham Trong Bach
5 tháng 7 2018

Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:

A. tan(α+β)=2cotα

B. tan(α+β)=2cotβ

C. tan(α+β)=2tanβ

D.tan(α+β)=2tanα
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
5 tháng 7 2018

Chọn đáp án B.

Đúng(0)
PT
Pham Trong Bach
14 tháng 2 2017
Phương trình sin x -3 cos x = 0 có nghiệm dạng x = a r c   cot m + k π ,   k ∈ ℤ  thì giá trị m là? A. m = -3 B.  m = 1 3 C. m = 3 D. m = 5...
Đọc tiếp

Phương trình sin x -3 cos x = 0 có nghiệm dạng x = a r c   cot m + k π ,   k ∈ ℤ  thì giá trị m là?

A. m = -3

B.  m = 1 3

C. m = 3

D. m = 5
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
14 tháng 2 2017

Đáp án là B

Đúng(0)
PT
Pham Trong Bach
9 tháng 4 2019
Số nghiệm thuộc ( 0 ;   π )  của phương trình sin   x + 1 +   c o s 2 x = 2 ( c o s 3 3 x + 1 ) là A. 1 B. 2 C. 3 D. 4...
Đọc tiếp

Số nghiệm thuộc ( 0 ;   π )  của phương trình sin   x + 1 +   c o s 2 x = 2 ( c o s 3 3 x + 1 ) là

A. 1

B. 2

C. 3

D. 4
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
9 tháng 4 2019

Đúng(0)
PT
Pham Trong Bach
4 tháng 7 2019
Hình phẳng giới hạn bởi đồ thị hàm số y = e x . sin x   và các đường thẳng x = 0, x = π, trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 , S 2 sao cho 2 S ...
Đọc tiếp

Hình phẳng giới hạn bởi đồ thị hàm số y = e x . sin x   và các đường thẳng x = 0, x = π, trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 , S 2 sao cho 2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2 khi đó k bằng:

A.  π 4

B.  π 2

C.  π 3

D.  π 6

#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
4 tháng 7 2019

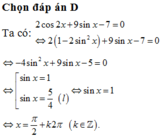
Ta có

S 1 = ∫ 0 k e x sin x d x ;   S 2 = ∫ k π e x sin x d x S = S 1 + S 2 = ∫ 0 π e x sin x d x

2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2

  ⇔ S 2 = 2 S 1 2 - 2 S 1 + 1 - S = 0 ⇔ 2 ∫ 0 k e x sin x d x 2 - 2 ∫ 0 k e x sin x d x + 1 - ∫ 0 k e x sin x d x = 0

Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2

Đáp án cần chọn là B

Đúng(0)
PT
Pham Trong Bach
2 tháng 6 2019
Hình phẳng giới hạn bởi đồ thị hàm số y = e x .   s i n x  và các đường thẳng x = 0 , x = π  ,trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 ; S 2 ...
Đọc tiếp

Hình phẳng giới hạn bởi đồ thị hàm số y = e x .   s i n x  và các đường thẳng x = 0 , x = π  ,trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 ; S 2  sao cho 2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2  khi đó k bằng:

A.  π 4

B.  π 2

C.  π 3

D.  π 6

#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
2 tháng 6 2019

Đáp án B

Đúng(0)
NH
Ngân Hoàng Xuân
6 tháng 3 2016

Cho \(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}\).tìm g trị nguyên lớn nhất của x để K có giá trị là số nguyên dương
#Hỏi cộng đồng OLM #Mẫu giáo
1
DT
Đinh Tuấn Việt
6 tháng 3 2016

Ta có :

\(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}=\frac{2\sqrt{x}-10}{\sqrt{x}-5}+\frac{13}{\sqrt{x}-5}=2+\frac{13}{\sqrt{x}-5}\)là số nguyên dương 

<=> 13 chia hết cho \(\sqrt{x}-5\)

<=> \(\sqrt{x}-5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)

<=> \(\sqrt{x}\in\left\{-12;4;6;18\right\}\)

<=> \(x\in\left\{16;36;324\right\}\) (vì \(\sqrt{x}\ge0\))

Do x nguyên và x có GTLN nên x = 324

Đúng(0)
PT
Pham Trong Bach
24 tháng 9 2019
Phương trình 2 sin 2 2 x − 5 sin 2 x + 2 = 0 có hai họ nghiệm dạng  x = α + kπ , x = β + kπ 0 < α , β < ...
Đọc tiếp

Phương trình 2 sin 2 2 x − 5 sin 2 x + 2 = 0 có hai họ nghiệm dạng  x = α + kπ , x = β + kπ 0 < α , β < π . Khi đó tích αβ  là

A. 5 π 2 36

B.  5 π 2 144

C. - 5 π 2 36

D.  - 5 π 2 144

#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
24 tháng 9 2019

Đúng(0)
PT
Pham Trong Bach
22 tháng 10 2019
Cho phương trình:  3 sin 2 x - cos 2 x = 4 sin   x - 1   . Tổng các nghiệm trong khoảng  - π ; π  của phương trình là: A.  π B.  π 6 C.  - 2 π 3 ...
Đọc tiếp

Cho phương trình:  3 sin 2 x - cos 2 x = 4 sin   x - 1   . Tổng các nghiệm trong khoảng  - π ; π  của phương trình là:

A.  π

B.  π 6

C.  - 2 π 3

D.  - π

#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
22 tháng 10 2019

Đáp án đúng : B

Đúng(0)
PT
Pham Trong Bach
4 tháng 10 2017
Số nghiệm thuộc khoảng ( 0 ; π )  của phương trình. tan   x + sin   x + tan   x - sin   x = 3 tan   x  là A. 0 B. 1 ...
Đọc tiếp

Số nghiệm thuộc khoảng ( 0 ; π )  của phương trình. tan   x + sin   x + tan   x - sin   x = 3 tan   x  là

A. 0

B. 1

C. 2

D. 3
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
4 tháng 10 2017

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP