Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì x=14 nên x+1=15
Thay 15=x+1 vào A(x) ta có:
A(x)= x15-(x+1)x14+(x+1)x13-(x+1)x12+...+(x+1)x3-(x+1)x2+(x+1)x-15
= x15-x15-x14+x14+x13-x13-x12+...+x4+x3-x3-x2+x2-x-15
= x-15
=> A(14) = 14-15=-1
Vậy A(14) = -1
b.* Với x=0 ta có:
0.f(-4)=-2.f(0)
=> 0=-2.f(0) => f(0)=0
=> đa thức f(x) có 1 nghiệm là 0 (1)
* với x=2 ta có: 2.f(-2)=0.f(2)
=> 2.f(2)=0 => f(2)=0
=> 2 là nghiệm của đa thức f(x) (2)
Từ (1) và (2) => đa thức f(x) có ít nhất 2 nghiệm

a) đề sai không làm đc
b)Với x=0
=>0.f(-4)=-2.f(0)
=>f(0)=0
=>x=0 là nghiệm của f(x)
Với x=2
=>2.f(-2)=0
=>f(-2)=0
=>-2 là nghiệm của f(x)
Vậy đpcm

a) Vì x=14 nên x+1=15
Thay 15=x+1 vào A(x) Ta có:
A(x)= x^15-(x+1)x^14+(x+1)x^13-(x+1)x^12+...+(x+1)x^3-(X+1)^2+(x+1)x-15
=x^15-x^15-x^14+x^14+x^13-x^13-...+X^4+x^3-X^3-x^2+x^2-x-15
=x-15
=> A(14)=14-15=-1
Vậy A(14)=-1
b) Với x=10 ta có
0.f(-4)=-2.f(0)
=>0=2.f(0) => f(0)=0
=> Đa thức f(x) có 1 nghiệm là 0 (1)
Với x =2 tao có: 2.f(-2)=0.(f) (2)
Từ (1) và (2)
=> Đa thức này có 2 nghiệm
k mình nha

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=4\\9a+b=-14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\a=-2\end{matrix}\right.\)

cho B(x) = 0
\(=>-5x+30=0\Rightarrow-5x=-30\Rightarrow x=6\)
cho E(x) = 0
\(=>x^2-81=0\Rightarrow x^2=81=>\left[{}\begin{matrix}x=9\\x=-9\end{matrix}\right.\)
cho C(x) = 0
\(=>2x+\dfrac{1}{3}=0=>2x=-\dfrac{1}{3}=>x=-\dfrac{1}{6}\)
bạn tham khảo hai câu này nha vì mình ko biết là mấy câu còn lại
B(x)=-5x+30
cho B(x)=0
=> -5x+30=0
-5x=-30
x=-30:(-5)
x=-6
* Vậy nghiệm của đa thức B(x) là -6.
C(x)=2x+1/3
cho C(x)=0
=>2x+1/3=0
2x=-1/3
x=-1/3:2
x=-1/6
vậy nghiệm của đa thức C(x) là -1/6.
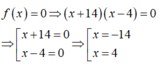
`(x+14).(x-4)`
`=>`\(\left[{}\begin{matrix}x+14=0\\x-4=0\end{matrix}\right.\)
`=>` \(\left[{}\begin{matrix}x=0-14=-14\\x=0+4=4\end{matrix}\right.\)
Vậy `x={-14;4}`
`=>` Chọn `D`
.