
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

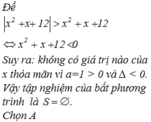

\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\3\left(x^2-4x\right)-\left(x-2\right)>12\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\3\left(x^2-4x\right)-\left(2-x\right)>12\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\3x^2-13x-10>0\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\3x^2-11x-14>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x>5\\x< -1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=5\end{matrix}\right.\)
3x2 - 12x - |x - 2| > 12
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\3x^2-12x-\left(x-2\right)>12\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\3x^2-12x-\left(2-x\right)>12\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge2\\3x^2-12x-x+2>12\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\3x^2-12x+x-2>12\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x>5\\x< -1\end{matrix}\right.\)
Vậy tập nghiệm là \(S=\left(-\infty;-1\right)\cup\left(5;+\infty\right)\)

\(\left(3-m\right)x>-m^2+4m-3\)
\(\Leftrightarrow\left(m-3\right)x< m^2-4m+3\)
\(\Leftrightarrow x< \dfrac{m^2-4m+3}{m-3}=m-1\)
Vậy \(x< m-1\)

Ta có tập nghiệm của phương trình là:
\(\left(x+2\right)\left(2x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\2x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Tập hợp S là:
\(S=\left\{-2;\dfrac{1}{2};3\right\}\)
Lần lược các phương án:
A. \(-2\in S\) (đúng)
B. \(3\in S\) (đúng)
C. \(2\in S\) (Sai)
D. \(\dfrac{1}{2}\in S\) (Đúng)
⇒ Chọn C

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

a, \(\dfrac{x-2}{x+1}\ge\dfrac{x+1}{x-2}\)
⇔ \(\dfrac{\left(x-2\right)^2-\left(x+1\right)^2}{\left(x-1\right)\left(x+2\right)}\ge0\)
⇔ \(\dfrac{3-6x}{\left(x+1\right)\left(x-2\right)}\) ≥ 0
⇔ \(\dfrac{2x-1}{\left(x+1\right)\left(x-2\right)}\) ≤ 0
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\-1< x< 2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\\left[{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}\le x< 2\\x< -1\end{matrix}\right.\)
Vậy tập nghiệm là \(\left(-\infty;-1\right)\cup\) \(\left[\dfrac{1}{2};2\right]\)\ {2}
Bạn có thể biến cái ngoặc vuông kia (ở chỗ số 2) thành ngoặc tròn
Còn vì sao mình không biến cái ngoặc vuông kia (ở chỗ số 2) thành ngoặc tròn thì đó là một câu chuyện dài
b, tương tự, chuyển vế đổi dấu