Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Đồ thị hàm số có 2 tiềm cận đứng
⇔ x ≥ − 1 x 2 − m x − 3 m = 0 có 2 nghiệm phân biệt.
⇔ x ≥ − 1 x 2 = m x + 3 ⇔ x ≥ − 1 m = x 2 x + 3 → f x = x 2 x + 3 có 2 nghiệm phân biệt
Xét hàm số f x = x 2 x + 3 trên − 1 ; + ∞ , có: f ' x = x x + 6 x + 3 2 ; f ' x = 0 ⇔ x = 0
Tính cách giác trị f − 1 = 1 2 ; f 0 = 0 và lim x → + ∞ f x = + ∞
Khi đó, yêu cầu * ⇔ m ∈ 0 ; 1 2 . Vậy m ∈ 0 ; 1 2 là giá trị cần tìm

Đáp án C
Ta có y = x 2 x 2 − 2 x − m + x + 1 x 2 − 4 x − m − 1
Điều kiện đặt ra là mẫu có 2 nghiệm => Δ ' = 5 + m > 0 < = > m > − 5

Chọn B
Điều kiện để đồ thị có tiệm cận: m ≠ - 3
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, I ∈ d ⇔ m = - 3 (loại). Vậy không tồn tại m thỏa mãn.

Chọn đáp án C
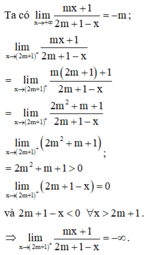
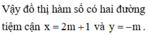
Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 3 suy ra
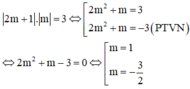

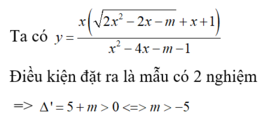


Đáp án B
Để đồ thị hàm số có hai đường tiệm cận đứng ⇔ x 2 − m x − 3 m = 0 có hai nghiệm phân biệt x 1 , x 2 ≥ − 1.
⇔ Δ > 0 x 1 + x 2 ≥ − 2 x 1 + 1 x 2 + 1 ≥ 0 ⇔ Δ = − m 2 − 4 − 3 m > 0 x 1 + x 2 ≥ − 2 x 1 x 2 + x 1 + x 2 + 1 ≥ 0 ⇔ m 2 + 12 m > 0 m ≥ − 2 1 − 2 m ≥ 0 ⇔ m ∈ 0 ; 1 2 .