Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Điều kiện để đồ thị có tiệm cận: m ≠ - 3
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, I ∈ d ⇔ m = - 3 (loại). Vậy không tồn tại m thỏa mãn.

Đáp án A
Ta có lim x → + ∞ y = lim x → − ∞ y = 1 nên đồ thị hàm số chỉ có duy nhất đường TCN y = 1

Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có 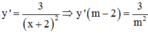
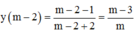
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: 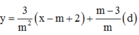
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2
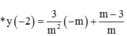
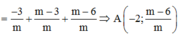
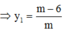
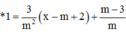
![]()
![]()
![]()
![]()
![]()
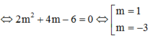
![]()

Đáp án C
Dễ thấy với m < 0 thì hàm không có tiệm
cận ngang vì x không tiến đến ∞
Với m = 0, hàm có dạng y = x + 1 và cũng
không có tiệm cận ngang
Với m > 0, ta có:
Xét lim x → + ∞ x + 1 m x 2 + 1 = lim x → + ∞ 1 + 1 x m + 1 x = 1 m
Lại có lim x → - ∞ x + 1 m x 2 + 1 = lim x → - ∞ 1 + 1 x - m + 1 x = 1 - m
⇒ Hàm có 2 tiệm cận ngang

Đáp án A
Ta có: lim x → + ∞ y = 0 ⇒ đồ thị hàm số có 1 tiệm cận ngang là y = 0 .
Để đồ thị hàm số có 3 tiệm cận thì phương trình : g x = x 2 − 2 m x + m + 2 = 0 có 2 nghiệm phân biệt
x 1 > x 2 ⇔ Δ ' = m 2 − m − 2 > 0 x 1 − 1 x 2 − 1 ≥ 0 x 1 − 1 + x 2 − 1 > 0 ⇔ m + 1 m − 2 > 0 x 1 x 2 − x 1 + x 2 + 1 ≥ 0 x 2 + x 2 > 2 ⇔ m + 1 m − 2 > 0 m + 2 − 2 m + 1 > 0 2 m > 2 ⇔ 3 ≥ m > 2.

Đáp án là D.
Đồ thị hàm số có bốn đường tiệm cận khi phương trình m 2 x 2 + m − 1 = 0 có hai nghiệm phân biệt khác -1 ⇔ m 2 ≠ 0 − m 2 m − 1 > 0 ⇔ m ≠ 0 m < 1 .


Đáp án D