Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Giả sử z = x + yi, (x,y ε R), khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.
a) Ta có |z| = 1 ⇔  = 1 ⇔ x2 + y2 = 1.
= 1 ⇔ x2 + y2 = 1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tam O, bán kính bằng 1
b) Ta có |z| ≤ 1 ⇔  ≤ 1 ⇔ x2 + y2 ≤ 1.
≤ 1 ⇔ x2 + y2 ≤ 1.
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn) (hình b)
c) Ta có 1 < |z| ≤ 2 ⇔ 1 <  ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này)
d) Ta có |z| = 1 ⇔  = 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1. Suy ra x = 0 và y = 1
= 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1. Suy ra x = 0 và y = 1
Vậy tập hợp các điểm cần tìm là điểm A(0;1)

Đặt \(z=a+bi\Rightarrow\overline{z}=a-bi\)
Ta có \(z.\overline{z}=1\Leftrightarrow\left(a+bi\right)\left(a-bi\right)=1\)
\(\Leftrightarrow a^2-b^2i^2=1\Leftrightarrow a^2+b^2=1\)
\(\Rightarrow\) Tập hợp các số phức thỏa mãn điều kiện trên là một đường tròn có tâm là gốc tọa độ, bán kính 1 đơn vị độ dài

Tập hợp các điểm biểu diễn các số phức z là các hình sau:
a) Ta có x = 1, y tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng x = 1 (hình a)
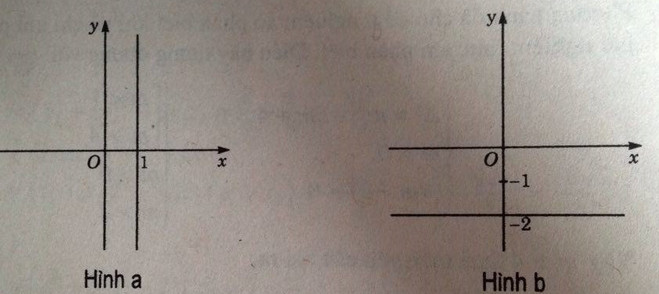
b) Ta có y = -2, x tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng y = -2 (hình b)
c) Ta có x ∈ [-1, 2] và y ∈ [0, 1] nên tập hợp các điểm biểu diễn z là hình chữ nhật sọc (hình c)
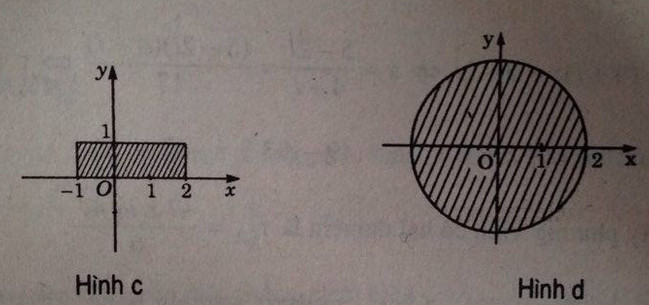
d) Ta có:
|z|≤2⇔√x2+y2≤2⇔x2+y2≤4|z|≤2⇔x2+y2≤2⇔x2+y2≤4
Vậy tập hợp các điểm biểu diễn z là hình tròn tâm O (gốc tọa độ) bán kính bằng 2 (kể cả các điểm trên đường tròn) (hình d)

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

mk nhầm câu c là 25f(x)
câu d là 24f(x)
mk nhầm nũa câu hỏi là cái f(x+2)-f(x) là bỏ nha

Giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực
Ta có:
\(|z-3+4i|=2\Leftrightarrow |(a-3)+i(b+4)|=2\)
\(\Leftrightarrow (a-3)^2+(b+4)^2=4\)
Vậy tập hợp các điểm biểu diễn số phức $z$ nằm trên đường tròn tâm \((3;-4)\) bán kính \(R=2\)
Chọn B.
Đặt z = a + bi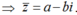
Theo giả thiết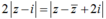 ⇔ 2|a + (b – 1)i| = |2(b + 1)i|
⇔ 2|a + (b – 1)i| = |2(b + 1)i|
Hay a2 + ( b - 1) 2 = ( b + 1)2
Suy ra: a2 = 4b
Quỹ tích các số phức z là một đường Parabol.