K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
31 tháng 5 2021
1.
ĐK: \(x\ne\dfrac{k\pi}{2}\)
\(cotx-tanx=sinx+cosx\)
\(\Leftrightarrow\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}=sinx+cosx\)
\(\Leftrightarrow\dfrac{cos^2x-sin^2x}{sinx.cosx}=sinx+cosx\)
\(\Leftrightarrow\left(\dfrac{cosx-sinx}{sinx.cosx}-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\cosx-sinx=sinx.cosx\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\)
\(\left(2\right)\Leftrightarrow t=\dfrac{1-t^2}{2}\left(t=cosx-sinx,\left|t\right|\le2\right)\)
\(\Leftrightarrow t^2+2t-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow cosx-sinx=-1+\sqrt{2}\)
\(\Leftrightarrow-\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=-1+\sqrt{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=-\dfrac{\pi}{4}+k\pi;x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi;x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\)
L
1) cosx\(^2\)+sinx=0
2) 2cos\(^2\)x-cos2x+cosx=0
3) sin\(^2\)x-3cos2x-2=0
4) tanx+\(\dfrac{2}{cotx}\)=0
2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
3.
\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)
\(\Leftrightarrow-7cos2x-3=0\)
\(\Rightarrow cos2x=-\dfrac{3}{7}\)
\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)
4.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(tanx+2tanx=0\)
\(\Rightarrow3tanx=0\)
\(\Rightarrow tanx=0\)
\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)
Vậy pt đã cho vô nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
1.
\(\Leftrightarrow1-sin^2x+sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))
2.
\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)
\(\Leftrightarrow cosx+1=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))
PT
1
CM
14 tháng 2 2019
Chọn C
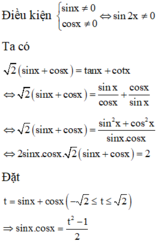
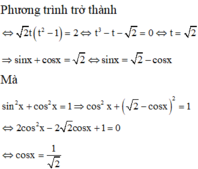
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đầu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:
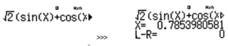
Tiếp theo ta tính cos x thì dễ thấy được:
Đến đây ta dễ dàng chọn được phương án C là phương án đúng thay cho lời giải tự luận nhiều phức tạp.
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 10 2020
1.
Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)
Pt trở thành:
\(t^3+\frac{t^2-1}{2}-1=0\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 10 2020
4.
Đặt \(sinx-cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{1-t^2}{2}\end{matrix}\right.\)
Pt trở thành:
\(t^3=1+\frac{1-t^2}{2}\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow...\)
5sin2x-12 (sinx-cosx) + 12 = 0
10sinxcosx-12sinx + 12cosx + 12 = 0
-5 (sinx-cosx) ²-12 (sinx-cosx) + 17 = 0
-5 (sinx-cosx) ²-17 (sinx-cosx) +5 (sinx-cosx) + 17 = 0
(5 (sinx-cosx) +17) (- (sinx-cosx) +1) = 0
sinx-cosx = 1 hoặc sinx-cosx = -17 / 5