K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
1
HP
9 tháng 9 2021
Làm lại:
ĐK: \(x\ne\dfrac{\pi}{2}+k\pi;x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2};x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(\dfrac{tan^23x-tan^2x}{1-tan^23x.tan^2x}=1\)
\(\Leftrightarrow\dfrac{tan3x-tanx}{1+tan3x.tanx}.\dfrac{tan3x+tanx}{1-tan3x.tanx}=1\)
\(\Leftrightarrow tan2x.tan4x=1\)
\(\Leftrightarrow\dfrac{sin2x.sin4x}{cos2x.cos4x}=1\)
\(\Leftrightarrow sin2x.sin4x=cos2x.cos4x\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos2x-cos6x\right)=\dfrac{1}{2}\left(cos6x+cos2x\right)\)
\(\Leftrightarrow cos6x=0\)
\(\Leftrightarrow6x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{6}\)
Đối chiếu với điều kiện rồi kết luận.
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2019
a/ \(tan3x=tanx\Rightarrow3x=x+k\pi\Rightarrow2x=k\pi\Rightarrow x=\frac{k\pi}{2}\)
b/ \(tan3x+tanx=0\Rightarrow tan3x=-tanx=tan\left(\pi-x\right)\)
\(\Rightarrow3x=\pi-x+k\pi\Rightarrow4x=\pi+k\pi\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{4}\)
c/ \(tan2x-tanx=0\Rightarrow tan2x=tanx\)
\(\Rightarrow2x=x+k\pi\Rightarrow x=k\pi\)
d/ \(tan2x+tanx=0\Rightarrow tan2x=-tanx=tan\left(\pi-x\right)\)
\(\Rightarrow2x=\pi-x+k\pi\Rightarrow3x=\pi+k\pi\Rightarrow x=\frac{\pi}{3}+\frac{k\pi}{3}\)
HP
1 tháng 9 2021
ĐK: \(x\ne-\dfrac{\pi}{4}+k\pi\)
\(\dfrac{tanx}{1-tan^2x}=\dfrac{1}{2}cot\left(x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\dfrac{2tanx}{1-tan^2x}=tan\left(\dfrac{\pi}{4}-x\right)\)
\(\Leftrightarrow tan2x=tan\left(\dfrac{\pi}{4}-x\right)\)
\(\Leftrightarrow2x=\dfrac{\pi}{4}-x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2020
1.
\(\Leftrightarrow3x=k\pi\Leftrightarrow x=\frac{k\pi}{3}\)
2.
\(\Leftrightarrow cos5x=0\Leftrightarrow5x=\frac{\pi}{2}+k\pi\Leftrightarrow x=\frac{\pi}{10}+\frac{k\pi}{5}\)
4.
\(cos3x+cosx+cos2x=0\)
\(\Leftrightarrow2cos2x.cosx+cos2x=0\)
\(\Leftrightarrow cos2x\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cosx=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2020
5.
\(sin6x+sin2x+sin4x=0\)
\(\Leftrightarrow2sin4x.cos2x+sin4x=0\)
\(\Leftrightarrow sin4x\left(2cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin4x=0\\cos2x=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{4}\\x=\pm\frac{\pi}{3}+k\pi\end{matrix}\right.\)
6. ĐKXĐ; ...
\(\Leftrightarrow tanx+tan2x=1-tanx.tan2x\)
\(\Leftrightarrow\frac{tanx+tan2x}{1-tanx.tan2x}=1\)
\(\Leftrightarrow tan3x=1\)
\(\Leftrightarrow x=\frac{\pi}{12}+\frac{k\pi}{3}\)
TV
2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2020
ĐKXĐ: ...
a.
\(\Leftrightarrow tan3x=tan\left(\frac{\pi}{4}\right)\)
\(\Leftrightarrow3x=\frac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{12}+\frac{k\pi}{3}\)
b.
\(cot4x=cot\left(-\frac{\pi}{6}\right)\)
\(\Leftrightarrow4x=-\frac{\pi}{6}+k\pi\)
\(\Leftrightarrow x=-\frac{\pi}{24}+\frac{k\pi}{4}\)
c.
\(\Leftrightarrow2x-\frac{\pi}{3}=\frac{\pi}{6}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \(\sqrt 3 \tan 2x = - 1\;\; \Leftrightarrow \tan 2x = - \frac{1}{{\sqrt 3 }}\;\;\; \Leftrightarrow \tan 2x = \tan - \frac{\pi }{6}\; \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \)
\(\;\; \Leftrightarrow x = - \frac{\pi }{{12}} + \frac{{k\pi }}{2}\;\left( {k \in \mathbb{Z}} \right)\)
b) \(\tan 3x + \tan 5x = 0\;\; \Leftrightarrow \tan 3x = \tan \left( { - 5x} \right) \Leftrightarrow 3x = - 5x + k\pi \;\; \Leftrightarrow 8x = k\pi \;\; \Leftrightarrow x = \frac{{k\pi }}{8}\;\left( {k \in \mathbb{Z}} \right)\)
PT
1
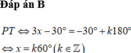
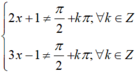
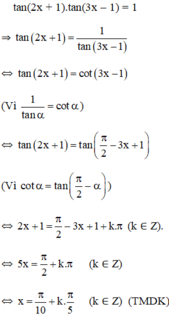
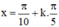(k ∈ Z).
\(\Rightarrow3x=2x+k\pi\Rightarrow x=k\pi\)