Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A C N M
a, xét tam giác ABC có CN là pg của ^ACB (gt)
=> BN/NA = BC/AC (Đl) (1)
xét tam giác ABC có AM là pg của ^BAC (gt)
=> BM/CM = AB/AC (đl) (2)
có BC = AB (gt) (3)
(1)(2)(3) => BN/NA = BM/CM
=> MN // AC (đl)

B1): a): +)Ta có csc đường cao BD, CE cắt nhau tại I => BD vg góc vs AC; CE vg góc vs AB
+)Xét tg AEC và tg ADB, có: AEC=AHB=90( BD vg góc vs AC; CE vg góc vs AB )
BAC chung
Do đó: tg AEC ~ tg ADB ( gg)
=> AE/AD= AC/AB=> AE*AB=AD*AC (đpcm)
b) : Gợi ý hoi :)): Kẻ đcao AF xuống BC, sẽ đi qua điểm I; c/m ED//BC=> c/m đc tg AED~tg ABC theo trường hợp cgc, từ đó ta sẽ có đc 2 góc AED = ABC ( vì 2 tg trên ~ vs nhau )
A B C 5 5 6 M N
a, Vì BM là phân giác ^B nên : \(\frac{AB}{BC}=\frac{AM}{MC}\)( t/c )
\(\Rightarrow\frac{MC}{BC}=\frac{AM}{AB}\)( tỉ lệ thức )
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{MC}{BC}=\frac{AM}{AB}=\frac{MC+AM}{BC+AB}=\frac{5}{11}\)
\(\Rightarrow\frac{MC}{6}=\frac{5}{11}\Rightarrow MC=\frac{30}{11}\)cm
\(\Rightarrow\frac{AM}{5}=\frac{5}{11}\Rightarrow AM=\frac{25}{11}\)cm

Ta có: ![]() (chứng minh trên)
(chứng minh trên)
Suy ra:![]()
Hay 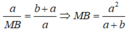
Trong ΔBAC, ta có:
MN //AC (chứng minh trên)
Và ![]()
Vậy 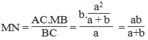

1: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\hat{AMB}=\hat{AMC}\)
mà \(\hat{AMB}+\hat{AMC}=180^0\) (hai góc kề bù)
nên \(\hat{AMB}=\hat{AMC}=\frac{180^0}{2}=90^0\)
=>AM⊥BC tại M
2: Xét ΔNAD và ΔNCM có
\(\hat{NAD}=\hat{NCM}\) (hai góc so le trong, AD//CM)
NA=NC
\(\hat{AND}=\hat{CNM}\) (hai góc đối đỉnh)
Do đó: ΔNAD=ΔNCM
=>AD=CM
Xét tứ giác AMCD có
AD//CM
AD=CM
do đó: AMCD là hình bình hành
Hình bình hành AMCD có \(\hat{AMC}=90^0\)
nên AMCD là hình chữ nhật
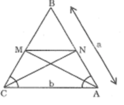



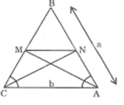
Trong △ BAC, ta có: AM là đường phân giác của (BAC)
Suy ra: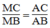 (tỉnh chất đường phân giác) (1)
(tỉnh chất đường phân giác) (1)
CN là đường phân giác của (BCA)
Suy ra: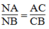 (tỉnh chất đường phân giác) (2)
(tỉnh chất đường phân giác) (2)
Lại có: AB = CB = a (gt)
Từ (1), (2) và (gt) suy ra: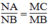
Trong △ BAC, ta có: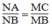
Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).